year
stringdate 1961-01-01 00:00:00
2025-01-01 00:00:00
⌀ | tier
stringclasses 5
values | problem_label
stringclasses 119
values | problem_type
stringclasses 13
values | exam
stringclasses 28
values | problem
stringlengths 87
2.77k
| solution
stringlengths 834
13k
| metadata
dict | problem_tokens
int64 50
903
| solution_tokens
int64 500
3.93k
|
|---|---|---|---|---|---|---|---|---|---|
1989
|
T1
|
2
| null |
APMO
|
Prove that the equation
$$
6\left(6 a^{2}+3 b^{2}+c^{2}\right)=5 n^{2}
$$
has no solutions in integers except $a=b=c=n=0$.
|
We can suppose without loss of generality that $a, b, c, n \geq 0$. Let $(a, b, c, n)$ be a solution with minimum sum $a+b+c+n$. Suppose, for the sake of contradiction, that $a+b+c+n>0$. Since 6 divides $5 n^{2}, n$ is a multiple of 6 . Let $n=6 n_{0}$. Then the equation reduces to
$$
6 a^{2}+3 b^{2}+c^{2}=30 n_{0}^{2}
$$
The number $c$ is a multiple of 3 , so let $c=3 c_{0}$. The equation now reduces to
$$
2 a^{2}+b^{2}+3 c_{0}^{2}=10 n_{0}^{2}
$$
Now look at the equation modulo 8:
$$
b^{2}+3 c_{0}^{2} \equiv 2\left(n_{0}^{2}-a^{2}\right) \quad(\bmod 8)
$$
Integers $b$ and $c_{0}$ have the same parity. Either way, since $x^{2}$ is congruent to 0 or 1 modulo 4 , $b^{2}+3 c_{0}^{2}$ is a multiple of 4 , so $n_{0}^{2}-a^{2}=\left(n_{0}-a\right)\left(n_{0}+a\right)$ is even, and therefore also a multiple of 4 , since $n_{0}-a$ and $n_{0}+a$ have the same parity. Hence $2\left(n_{0}^{2}-a^{2}\right)$ is a multiple of 8 , and
$$
b^{2}+3 c_{0}^{2} \equiv 0 \quad(\bmod 8)
$$
If $b$ and $c_{0}$ are both odd, $b^{2}+3 c_{0}^{2} \equiv 4(\bmod 8)$, which is impossible. Then $b$ and $c_{0}$ are both even. Let $b=2 b_{0}$ and $c_{0}=2 c_{1}$, and we find
$$
a^{2}+2 b_{0}^{2}+6 c_{1}^{2}=5 n_{0}^{2}
$$
Look at the last equation modulo 8:
$$
a^{2}+3 n_{0}^{2} \equiv 2\left(c_{1}^{2}-b_{0}^{2}\right) \quad(\bmod 8)
$$
A similar argument shows that $a$ and $n_{0}$ are both even.
We have proven that $a, b, c, n$ are all even. Then, dividing the original equation by 4 we find
$$
6\left(6(a / 2)^{2}+3(b / 2)^{2}+(c / 2)^{2}\right)=5(n / 2)^{2}
$$
and we find that $(a / 2, b / 2, c / 2, n / 2)$ is a new solution with smaller sum. This is a contradiction, and the only solution is $(a, b, c, n)=(0,0,0,0)$.
|
{
"problem_match": "# Problem 2",
"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl",
"solution_match": "# Solution\n\n"
}
| 51
| 749
|
1989
|
T1
|
3
| null |
APMO
|
Let $A_{1}, A_{2}, A_{3}$ be three points in the plane, and for convenience,let $A_{4}=A_{1}, A_{5}=A_{2}$. For $n=1,2$, and 3 , suppose that $B_{n}$ is the midpoint of $A_{n} A_{n+1}$, and suppose that $C_{n}$ is the midpoint of $A_{n} B_{n}$. Suppose that $A_{n} C_{n+1}$ and $B_{n} A_{n+2}$ meet at $D_{n}$, and that $A_{n} B_{n+1}$ and $C_{n} A_{n+2}$ meet at $E_{n}$. Calculate the ratio of the area of triangle $D_{1} D_{2} D_{3}$ to the area of triangle $E_{1} E_{2} E_{3}$.
Answer: $\frac{25}{49}$.
|
Let $G$ be the centroid of triangle $A B C$, and also the intersection point of $A_{1} B_{2}, A_{2} B_{3}$, and $A_{3} B_{1}$ 。
By Menelao's theorem on triangle $B_{1} A_{2} A_{3}$ and line $A_{1} D_{1} C_{2}$,
$$
\frac{A_{1} B_{1}}{A_{1} A_{2}} \cdot \frac{D_{1} A_{3}}{D_{1} B_{1}} \cdot \frac{C_{2} A_{2}}{C_{2} A_{3}}=1 \Longleftrightarrow \frac{D_{1} A_{3}}{D_{1} B_{1}}=2 \cdot 3=6 \Longleftrightarrow \frac{D_{1} B_{1}}{A_{3} B_{1}}=\frac{1}{7}
$$
Since $A_{3} G=\frac{2}{3} A_{3} B_{1}$, if $A_{3} B_{1}=21 t$ then $G A_{3}=14 t, D_{1} B_{1}=\frac{21 t}{7}=3 t, A_{3} D_{1}=18 t$, and $G D_{1}=A_{3} D_{1}-A_{3} G=18 t-14 t=4 t$, and
$$
\frac{G D_{1}}{G A_{3}}=\frac{4}{14}=\frac{2}{7}
$$
Similar results hold for the other medians, therefore $D_{1} D_{2} D_{3}$ and $A_{1} A_{2} A_{3}$ are homothetic with center $G$ and ratio $-\frac{2}{7}$.
By Menelao's theorem on triangle $A_{1} A_{2} B_{2}$ and line $C_{1} E_{1} A_{3}$,
$$
\frac{C_{1} A_{1}}{C_{1} A_{2}} \cdot \frac{E_{1} B_{2}}{E_{1} A_{1}} \cdot \frac{A_{3} A_{2}}{A_{3} B_{2}}=1 \Longleftrightarrow \frac{E_{1} B_{2}}{E_{1} A_{1}}=3 \cdot \frac{1}{2}=\frac{3}{2} \Longleftrightarrow \frac{A_{1} E_{1}}{A_{1} B_{2}}=\frac{2}{5}
$$
If $A_{1} B_{2}=15 u$, then $A_{1} G=\frac{2}{3} \cdot 15 u=10 u$ and $G E_{1}=A_{1} G-A_{1} E_{1}=10 u-\frac{2}{5} \cdot 15 u=4 u$, and
$$
\frac{G E_{1}}{G A_{1}}=\frac{4}{10}=\frac{2}{5}
$$
Similar results hold for the other medians, therefore $E_{1} E_{2} E_{3}$ and $A_{1} A_{2} A_{3}$ are homothetic with center $G$ and ratio $\frac{2}{5}$.
Then $D_{1} D_{2} D_{3}$ and $E_{1} E_{2} E_{3}$ are homothetic with center $G$ and ratio $-\frac{2}{7}: \frac{2}{5}=-\frac{5}{7}$, and the ratio of their area is $\left(\frac{5}{7}\right)^{2}=\frac{25}{49}$.
|
{
"problem_match": "# Problem 3",
"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl",
"solution_match": "\nSolution\n"
}
| 219
| 864
|
1989
|
T1
|
4
| null |
APMO
|
Let $S$ be a set consisting of $m$ pairs $(a, b)$ of positive integers with the property that $1 \leq a<$ $b \leq n$. Show that there are at least
$$
4 m \frac{\left(m-\frac{n^{2}}{4}\right)}{3 n}
$$
triples $(a, b, c)$ such that $(a, b),(a, c)$, and $(b, c)$ belong to $S$.
|
Call a triple $(a, b, c)$ good if and only if $(a, b),(a, c)$, and $(b, c)$ all belong to $S$. For $i$ in $\{1,2, \ldots, n\}$, let $d_{i}$ be the number of pairs in $S$ that contain $i$, and let $D_{i}$ be the set of numbers paired with $i$ in $S$ (so $\left|D_{i}\right|=d_{i}$ ). Consider a pair $(i, j) \in S$. Our goal is to estimate the number of integers $k$ such that any permutation of $\{i, j, k\}$ is good, that is, $\left|D_{i} \cap D_{j}\right|$. Note that $i \notin D_{i}$ and $j \notin D_{j}$, so $i, j \notin D_{i} \cap D_{j}$; thus any $k \in D_{i} \cap D_{j}$ is different from both $i$ and $j$, and $\{i, j, k\}$ has three elements as required. Now, since $D_{i} \cup D_{j} \subseteq\{1,2, \ldots, n\}$,
$$
\left|D_{i} \cap D_{j}\right|=\left|D_{i}\right|+\left|D_{j}\right|-\left|D_{i} \cup D_{j}\right| \leq d_{i}+d_{j}-n
$$
Summing all the results, and having in mind that each good triple is counted three times (one for each two of the three numbers), the number of good triples $T$ is at least
$$
T \geq \frac{1}{3} \sum_{(i, j) \in S}\left(d_{i}+d_{j}-n\right)
$$
Each term $d_{i}$ appears each time $i$ is in a pair from $S$, that is, $d_{i}$ times; there are $m$ pairs in $S$, so $n$ is subtracted $m$ times. By the Cauchy-Schwartz inequality
$$
T \geq \frac{1}{3}\left(\sum_{i=1}^{n} d_{i}^{2}-m n\right) \geq \frac{1}{3}\left(\frac{\left(\sum_{i=1}^{n} d_{i}\right)^{2}}{n}-m n\right) .
$$
Finally, the sum $\sum_{i=1}^{n} d_{i}$ is $2 m$, since $d_{i}$ counts the number of pairs containing $i$, and each pair $(i, j)$ is counted twice: once in $d_{i}$ and once in $d_{j}$. Therefore
$$
T \geq \frac{1}{3}\left(\frac{(2 m)^{2}}{n}-m n\right)=4 m \frac{\left(m-\frac{n^{2}}{4}\right)}{3 n} .
$$
Comment: This is a celebrated graph theory fact named Goodman's bound, after A. M. Goodman's method published in 1959. The generalized version of the problem is still studied to this day.
|
{
"problem_match": "# Problem 4",
"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl",
"solution_match": "# Solution\n\n"
}
| 104
| 742
|
1989
|
T1
|
5
| null |
APMO
|
Determine all functions $f$ from the reals to the reals for which
(1) $f(x)$ is strictly increasing,
(2) $f(x)+g(x)=2 x$ for all real $x$, where $g(x)$ is the composition inverse function to $f(x)$.
(Note: $f$ and $g$ are said to be composition inverses if $f(g(x))=x$ and $g(f(x))=x$ for all real x.)
Answer: $f(x)=x+c, c \in \mathbb{R}$ constant.
|
Denote by $f_{n}$ the $n$th iterate of $f$, that is, $f_{n}(x)=\underbrace{f(f(\ldots f}_{n \text { times }}(x)))$.
Plug $x \rightarrow f_{n+1}(x)$ in (2): since $g\left(f_{n+1}(x)\right)=g\left(f\left(f_{n}(x)\right)\right)=f_{n}(x)$,
$$
f_{n+2}(x)+f_{n}(x)=2 f_{n+1}(x)
$$
that is,
$$
f_{n+2}(x)-f_{n+1}(x)=f_{n+1}(x)-f_{n}(x)
$$
Therefore $f_{n}(x)-f_{n-1}(x)$ does not depend on $n$, and is equal to $f(x)-x$. Summing the corresponding results for smaller values of $n$ we find
$$
f_{n}(x)-x=n(f(x)-x) .
$$
Since $g$ has the same properties as $f$,
$$
g_{n}(x)-x=n(g(x)-x)=-n(f(x)-x) .
$$
Finally, $g$ is also increasing, because since $f$ is increasing $g(x)>g(y) \Longrightarrow f(g(x))>$ $f(g(y)) \Longrightarrow x>y$. An induction proves that $f_{n}$ and $g_{n}$ are also increasing functions.
Let $x>y$ be real numbers. Since $f_{n}$ and $g_{n}$ are increasing,
$$
x+n(f(x)-x)>y+n(f(y)-y) \Longleftrightarrow n[(f(x)-x)-(f(y)-y)]>y-x
$$
and
$$
x-n(f(x)-x)>y-n(f(y)-y) \Longleftrightarrow n[(f(x)-x)-(f(y)-y)]<x-y
$$
Summing it up,
$$
|n[(f(x)-x)-(f(y)-y)]|<x-y \quad \text { for all } n \in \mathbb{Z}_{>0}
$$
Suppose that $a=f(x)-x$ and $b=f(y)-y$ are distinct. Then, for all positive integers $n$,
$$
|n(a-b)|<x-y
$$
which is false for a sufficiently large $n$. Hence $a=b$, and $f(x)-x$ is a constant $c$ for all $x \in \mathbb{R}$, that is, $f(x)=x+c$.
It is immediate that $f(x)=x+c$ satisfies the problem, as $g(x)=x-c$.
|
{
"problem_match": "# Problem 5",
"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl",
"solution_match": "# Solution\n\n"
}
| 123
| 598
|
1990
|
T1
|
1
| null |
APMO
|
In $\triangle A B C$, let $D, E, F$ be the midpoints of $B C, A C, A B$ respectively and let $G$ be the centroid of the triangle.
For each value of $\angle B A C$, how many non-similar triangles are there in which $A E G F$ is a cyclic quadrilateral?
|
Let $I$ be the intersection of $A G$ and $E F$.
Let $\delta=A I . I G-F I$ IE. Then
$$
A I=A D / 2, \quad I G=A D / 6, \quad F I=B C / 4=I E
$$
Further, applying the cosine rule to triangles $A B D, A C D$ we get
$$
\begin{aligned}
A B^{2} & =B C^{2} / 4+A D^{2}-A D \cdot B C \cdot \cos \angle B D A, \\
A C^{2} & =B C^{2} / 4+A D^{2}+A D \cdot B C \cdot \cos \angle B D A, \\
\text { so } \quad A D^{2} & =\left(A B^{2}+A C^{2}-B C^{2} / 2\right) / 2
\end{aligned}
$$
Hence
$$
\begin{aligned}
\delta & =\left(A B^{2}+A C^{2}-2 B C^{2}\right) / 24 \\
& =\left(4 A B \cdot A C \cdot \cos \angle B A C-A B^{2}-A C^{2}\right)
\end{aligned}
$$
Now $A E F G$ is a cyclic quadrilateral if and only if $\delta=0$, i.e. if and only if
$$
\begin{aligned}
\cos \angle B A C & =\left(A B^{2}+A B^{2}\right) /(4 \cdot A B \cdot A C) \\
& =(A B / A C+A C / A B) / 4
\end{aligned}
$$
5
Now $A B / A C+A C / A B \geq 2$. Hence $\cos \angle B A C \geq 1 / 2$ and so $\angle B A C \leq 60^{\circ}$.
For $\angle B A C>60^{\circ}$ there is no triangle with the required property.
For $\angle B A C=60^{\circ}$ there exists, within similarity, precisely one triangle (which is equilateral) having the required property.
For $\angle B A C<60^{\circ}$ there exists, within similarity, again precisely one triangle having the required property (even though for fixed median $A E$ there are two, but one arises from the other by interchanging point $B$ with point $C$, thus proving them to be similar).
|
{
"problem_match": "# Question 1 ",
"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl",
"solution_match": "# FIRST SOLUTION\n\n"
}
| 75
| 571
|
1990
|
T1
|
1
| null |
APMO
|
In $\triangle A B C$, let $D, E, F$ be the midpoints of $B C, A C, A B$ respectively and let $G$ be the centroid of the triangle.
For each value of $\angle B A C$, how many non-similar triangles are there in which $A E G F$ is a cyclic quadrilateral?
|
in the figure as shown below, we first show that it is necessary that $\angle A$ is less than $90^{\circ}$ if the quadrilateral $A E G F$ ; cyclic.
Now, since $E F \| B C$, we get
$$
\begin{aligned}
\angle E G F & =180^{\circ}-\left(B_{1}+C_{1}\right) \\
& \geq 180^{\circ}-(B+C) \\
& =A .
\end{aligned}
$$
(1)
Thus, if $A E G F$ is cyclic, we would have $\angle E G F+\angle A=180^{\circ}$. Therefore it is necessary that $0<\angle A \leq 90^{\circ}$.
## Continuation "A"
Let $O$ be the circumcentre of $\triangle A F E$. Without loss of generality, let the radius of this circle be 1.
We then let $A=1, F=z=e^{i \theta}$ and $E=z e^{2 i \alpha}=e^{i(\theta+2 \alpha)}$.
Then $\angle A=\alpha, 0<\alpha \leq 90^{\circ}$, and $0<\theta<360^{\circ}-2 \alpha$.
Thus,
$$
B=2 z-1
$$
and
$$
\begin{aligned}
G & =\frac{1}{3}(2 z-1)+\frac{2}{3}\left(z e^{2 i \alpha}\right) \\
& =\frac{1}{3}\left(2 e^{i \theta}+2 e^{i(\theta+2 \alpha)}-1\right)
\end{aligned}
$$
For quadrilateral $A F G E$ to be cyclic, it is now necessary that
$$
|G|=1 .
$$
For $|G|=1$, we must have
$$
\begin{aligned}
9= & (2 \cos (\theta)+2 \cos (\theta+2 \alpha)-1)^{2}+(2 \sin (\theta)+2 \sin (\theta+2 \alpha))^{2} \\
= & 4\left(\cos ^{2}(\theta)+\sin ^{2}(\theta)\right)+4\left(\cos ^{2}(\theta+2 \alpha)+\sin ^{2}(\theta+2 \alpha)\right)+1 \\
& +8(\cos (\theta) \cos (\theta+2 \alpha)+\sin (\theta) \sin (\theta+2 \alpha))-4 \cos (\theta)-4 \cos (\theta+2 \alpha) \\
= & 9+8 \cos (2 \alpha)-8 \cos (\alpha) \cos (\theta+\alpha)
\end{aligned}
$$
so that
$$
\cos (\theta+\alpha)=\frac{\cos (2 \alpha)}{\cos (\alpha)}
$$
] Now, $\left|\frac{\cos (2 \alpha)}{\cos (\alpha)}\right| \leq 1$ if and only if $\alpha \in\left(0,60^{\circ}\right]$ in the range of $\alpha$ under consideration, that is $\alpha \in\left(0,00^{\circ}\right]$. There is equality if and only if $\alpha=60^{\circ}$.
$\square$ Note there is only one solution. The apparent other solution is the mirror image of the first. We are solving for $\alpha+\theta$. The other solution is $360^{\circ}-\alpha-\theta$.
## Continuation "B"
Let $O$ be the circumcentre of triangle $A E F$. Let $A P$ be a diameter of this circle. Construct the circle with centre $P$ and radius $A P$. Then $B$ and $C$ lie on this circle.
It is clear that the problem is solved if we allow the angle $\angle B A C=\alpha$ to vary and restrict $B$ and $C$ to the constructed circle.
Let $\theta$ be the angle from the drawn axis. Then $\theta$ lies in the range $\left(0,180^{\circ}-\alpha\right)$. We must not forget the necessary restriction of $\alpha$, that is $\alpha \in\left(0,90^{\circ}\right.$.
Now, $D$ lies on an arc of a circle, centre $P$, radius $P D$ exterior to the circle, centre $O$, radius $A O$.
By similarity, $G$, lies on an arc of a circle, centre $Q$, radius $Q G$ where $A Q=\frac{2}{3} A P$ and $Q G=\frac{2}{3} P D$.
For the quadrilateral $A F G E$ to be cyclic, we must have that the radius $Q G$ is greater than or equal to $Q P$.
The easiest way to calulate these radii is to consider the case in which the diameter $A P$ bisects the angle $\angle B A C$.
Thus we re-draw the diagram as below. Let $A H$ be a diameter of the larger circle.
Thus we have $A H=4$ and by similar triangles,
$$
\frac{A D}{A B}=\frac{A B}{A H}=\cos \left(\frac{\alpha}{2}\right)
$$
so that
$$
\begin{aligned}
A D & =4 \cos ^{2}\left(\frac{\alpha}{2}\right) \\
& =2+2 \cos (\alpha) .
\end{aligned}
$$
Thus $P D=2 \cos (\alpha)$ and $Q G=\frac{2}{3} 2 \cos (\alpha)=\frac{4}{3} \cos (\alpha)$.
The necessary condition for a cyclic quadrilateral is then
$$
\frac{4}{3}(1+\cos (\alpha)) \geq 2
$$
[5
$$
\cos (\alpha) \geq \frac{1}{2}
$$
:7
Thus it is clear that there is precisely one (up to similarity) solution for $0<\alpha \leq 60^{\circ}$ and no solutions otherwise.
|
{
"problem_match": "# Question 1 ",
"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl",
"solution_match": "\nTHIRD SOLUTION\n"
}
| 75
| 1,379
|
1990
|
T1
|
2
| null |
APMO
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers, and let $S_{k}$ be the sum of products of $a_{1}, a_{2}, \ldots, a_{n}$ taken $k$ at a time.
Show that
$$
S_{k} S_{n-k} \geq\binom{ n}{k}^{2} a_{1} a_{2} \ldots a_{n}, \quad \text { for } \quad k=1,2, \ldots, n-1
$$
|
(provided by the Canadian Problems Committee).
Write $S_{k}$ as $\sum_{i=1}^{\binom{n}{k}} t_{i}$. Then
주
$$
S_{n-k}=\left(\prod_{m=1}^{n} a_{m}\right)\left(\sum_{i=1}^{\binom{n}{k}} \frac{1}{t_{i}}\right)
$$
$$
\text { so that } \left.\begin{array}{rl}
S_{k} S_{n-k} & =\left(\prod_{m=1}^{n} a_{m}\right) \cdot\left(\begin{array}{l}
\binom{n}{k} \\
i=1
\end{array} t_{i}\right)\left(\begin{array}{l}
\binom{n}{k} \\
\sum_{j=1}^{2}
\end{array} \frac{1}{t_{j}}\right) \\
& =\left(\prod_{m=1}^{n} a_{m}\right)\left[\sum_{i=1}^{\binom{n}{k}} 1+\sum_{i=1}^{\binom{n}{k}} \sum_{j=1}^{n} \begin{array}{l}
n \\
k
\end{array}\right) \\
\frac{t_{i}}{} \\
t_{j}
\end{array}\right] .
$$
As there are
$$
\frac{\binom{n}{k}^{2}-\binom{n}{k}}{2}
$$
terms in the sum
$$
\begin{aligned}
S_{k} S_{n-k} & \geq\left(\prod_{m=1}^{n} a_{m}\right)\left[\binom{n}{k}+2 \cdot \frac{\binom{n}{k}^{2}-\binom{n}{k}}{2}\right] \\
& =\binom{n}{k}^{2}\left(\prod_{m=1}^{n} a_{m}\right)
\end{aligned}
$$
since $\frac{t_{i}}{t_{j}}+\frac{t_{j}}{t_{i}} \geq 2$ for $t_{i}, t_{j}>0$.
|
{
"problem_match": "# Question 2",
"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl",
"solution_match": "\nSECOND SOLUTION "
}
| 128
| 512
|
1990
|
T1
|
4
| null |
APMO
|
A set of 1990 persons is divided into non-intersecting subsets in such a way that
(a) no one in a subset knows all the others in the subset;
(b) among any three persons in a subset, there are always at least two who do not know each other; and
(c) for any two persons in a subset who do not know each other, there is exactly one person in the same subset knowing both of them.
(i) Prove that within each subset, every person has the same number of acquaintances.
(ii) Determine the maximum possible number of subsets.
Note: it is understood that if a person $A$ knows person $B$, then person $B$ will know person $A$; an acquaintance is someone who is known. Every person is assumed to know one's self.
|
(i) Let $S$ be a subset of persons satisfying conditions (a), (b) and (c). Let $x \in S$ be one who knows the maximum number of persons in $S$.
Assume that $x$ knows $x_{1}, x_{2}, \ldots, x_{n}$. By (b), $x_{i}$ and $x_{j}$ are strangers if $i \neq j$. For each $x_{i}$, let $N_{i}$ be the set of persons in $S$ who know $x_{i}$ but not $x$. Note that, for $i \neq j, N_{i}$ has no person in common with $N_{j}$, otherwise there would be more than one person knowing $x_{i}$ and $x_{j}$, contradicting (c).
By (a) we may assume that $N_{1}$ is not empty.) Let $y_{1} \in N_{1}$. By (c), for each $k>1$, there is exactly one person $y_{k}$ in $N_{k}$ who knows $y_{1}$. This means that $y_{1}$ knows $n$ persons, namely $x_{1}, y_{2}, \ldots, y_{n}$.
Because $n$ is the maximal number of persons in $S$ a person in $S$ can know, $y_{1}$ knows exactly $n$ persons in $S$. By precisely the same reasoning we find that each person in $N_{i}$, $i=1,2, \ldots, n$, knows exactly $n$ persons in $S$.
Letting $y_{1}$ take the role of $x$ in our argument, we see that also each $x_{i}$ knows exactly $n$ persons. Note that, by (c), every person in $S$ other than $x, x_{1}, \ldots, x_{n}$, must be in some $N_{j}$. Therefore every person in $S$ knows exactly $n$ persons in $S$ and thus has the same number of acquaintances in $S$.
(ii) To maximize the number of subsets, we have to minimize the size of each group. The smallest possible subset is one in which every person knows exactly two persons, and hence there must be exactly five persons in the subset, forming a cycle where two persons stand side by side only if they know each other. Therefore the maximum possible number of subsets is 1990/5 $=398$.
|
{
"problem_match": "# Question 4",
"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl",
"solution_match": "# SOLUTION:"
}
| 169
| 550
|
1991
|
T1
|
4
| null |
APMO
|
During a break, $n$ children at school sit in a circle around their teacher to play a game. The teacher walks clockwise close to the children and hands out candies to some of them according to the following rule. He selects one child and gives him a candy, then he skips the next child and gives a candy to the next one, then he skips 2 and gives a candy to the next one, then he skips 3, and soon. Determine the values of $n$ for which eventually, perhaps after many rounds, all children will have at least one candy each.
Answer: All powers of 2 .
|
Number the children from 0 to $n-1$. Then the teacher hands candy to children in positions $f(x)=1+2+\cdots+x \bmod n=\frac{x(x+1)}{2} \bmod n$. Our task is to find the range of $f: \mathbb{Z}_{n} \rightarrow \mathbb{Z}_{n}$, and to verify whether the range is $\mathbb{Z}_{n}$, that is, whether $f$ is a bijection.
If $n=2^{a} m, m>1$ odd, look at $f(x)$ modulo $m$. Since $m$ is odd, $m|f(x) \Longleftrightarrow m| x(x+1)$. Then, for instance, $f(x) \equiv 0(\bmod m)$ for $x=0$ and $x=m-1$. This means that $f(x)$ is not a bijection modulo $m$, and there exists $t$ such that $f(x) \not \equiv t(\bmod m)$ for all $x$. By the Chinese Remainder Theorem,
$$
f(x) \equiv t \quad(\bmod n) \Longleftrightarrow \begin{cases}f(x) \equiv t & \left(\bmod 2^{a}\right) \\ f(x) \equiv t & (\bmod m)\end{cases}
$$
Therefore, $f$ is not a bijection modulo $n$.
If $n=2^{a}$, then
$$
f(x)-f(y)=\frac{1}{2}(x(x+1)-y(y+1))=\frac{1}{2}\left(x^{2}-y^{2}+x-y\right)=\frac{(x-y)(x+y+1)}{2} .
$$
and
$$
f(x) \equiv f(y) \quad\left(\bmod 2^{a}\right) \Longleftrightarrow(x-y)(x+y+1) \equiv 0 \quad\left(\bmod 2^{a+1}\right)
$$
If $x$ and $y$ have the same parity, $x+y+1$ is odd and $(*)$ is equivalent to $x \equiv y\left(\bmod 2^{a+1}\right)$. If $x$ and $y$ have different parity,
$$
(*) \Longleftrightarrow x+y+1 \equiv 0 \quad\left(\bmod 2^{a+1}\right)
$$
However, $1 \leq x+y+1 \leq 2\left(2^{a}-1\right)+1=2^{a+1}-1$, so $x+y+1$ is not a multiple of $2^{a+1}$. Therefore $f$ is a bijection if $n$ is a power of 2 .
|
{
"problem_match": "# Problem 4",
"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl",
"solution_match": "# Solution 1"
}
| 126
| 619
|
1991
|
T1
|
4
| null |
APMO
|
During a break, $n$ children at school sit in a circle around their teacher to play a game. The teacher walks clockwise close to the children and hands out candies to some of them according to the following rule. He selects one child and gives him a candy, then he skips the next child and gives a candy to the next one, then he skips 2 and gives a candy to the next one, then he skips 3, and soon. Determine the values of $n$ for which eventually, perhaps after many rounds, all children will have at least one candy each.
Answer: All powers of 2 .
|
We give a full description of $a_{n}$, the size of the range of $f$.
Since congruences modulo $n$ are defined, via Chinese Remainder Theorem, by congruences modulo $p^{\alpha}$ for all prime divisors $p$ of $n$ and $\alpha$ being the number of factors $p$ in the factorization of $n, a_{n}=\prod_{p^{\alpha} \| n} a_{p^{\alpha}}$.
Refer to the first solution to check the case $p=2: a_{2^{\alpha}}=2^{\alpha}$.
For an odd prime $p$,
$$
f(x)=\frac{x(x+1)}{2}=\frac{(2 x+1)^{2}-1}{8}
$$
and since $p$ is odd, there is a bijection between the range of $f$ and the quadratic residues modulo $p^{\alpha}$, namely $t \mapsto 8 t+1$. So $a_{p^{\alpha}}$ is the number of quadratic residues modulo $p^{\alpha}$.
Let $g$ be a primitive root of $p^{\alpha}$. Then there are $\frac{1}{2} \phi\left(p^{\alpha}\right)=\frac{p-1}{2} \cdot p^{\alpha-1}$ quadratic residues that are coprime with $p: 1, g^{2}, g^{4}, \ldots, g^{\phi\left(p^{n}\right)-2}$. If $p$ divides a quadratic residue $k p$, that is, $x^{2} \equiv k p$ $\left(\bmod p^{\alpha}\right), \alpha \geq 2$, then $p$ divides $x$ and, therefore, also $k$. Hence $p^{2}$ divides this quadratic residue, and these quadratic residues are $p^{2}$ times each quadratic residue of $p^{\alpha-2}$. Thus
$$
a_{p^{\alpha}}=\frac{p-1}{2} \cdot p^{\alpha-1}+a_{p^{\alpha}-2} .
$$
Since $a_{p}=\frac{p-1}{2}+1$ and $a_{p^{2}}=\frac{p-1}{2} \cdot p+1$, telescoping yields
$$
a_{p^{2 t}}=\frac{p-1}{2}\left(p^{2 t-1}+p^{2 t-3}+\cdots+p\right)+1=\frac{p\left(p^{2 t}-1\right)}{2(p+1)}+1
$$
and
$$
a_{p^{2 t-1}}=\frac{p-1}{2}\left(p^{2 t-2}+p^{2 t-4}+\cdots+1\right)+1=\frac{p^{2 t}-1}{2(p+1)}+1
$$
Now the problem is immediate: if $n$ is divisible by an odd prime $p, a_{p^{\alpha}}<p^{\alpha}$ for all $\alpha$, and since $a_{t} \leq t$ for all $t, a_{n}<n$.
|
{
"problem_match": "# Problem 4",
"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl",
"solution_match": "# Solution 2"
}
| 126
| 717
|
1992
|
T1
|
3
| null |
APMO
|
Let $n$ be an integer such that $n>3$. Suppose that we choose three numbers from the set $\{1,2, \ldots, n\}$. Using each of these three numbers only once and using addition, multiplication, and parenthesis, let us form all possible combinations.
(a) Show that if we choose all three numbers greater than $n / 2$, then the values of these combinations are all distinct.
(b) Let $p$ be a prime number such that $p \leq \sqrt{n}$. Show that the number of ways of choosing three numbers so that the smallest one is $p$ and the values of the combinations are not all distinct is precisely the number of positive divisors of $p-1$.
|
In both items, the smallest chosen number is at least 2: in part (a), $n / 2>1$ and in part (b), $p$ is a prime. So let $1<x<y<z$ be the chosen numbers. Then all possible combinations are
$$
x+y+z, \quad x+y z, \quad x y+z, \quad y+z x, \quad(x+y) z, \quad(z+x) y, \quad(x+y) z, \quad x y z
$$
Since, for $1<m<n$ and $t>1,(m-1)(n-1) \geq 1 \cdot 2 \Longrightarrow m n>m+n, t n+m-(t m+n)=$ $(t-1)(n-m)>0 \Longrightarrow t n+m>t m+n$, and $(t+m) n-(t+n) m=t(n-m)>0$,
$$
x+y+z<z+x y<y+z x<x+y z
$$
and
$$
(y+z) x<(x+z) y<(x+y) z<x y z .
$$
Also, $(y+z) x-(y+z x)=(x-1) y>0 \Longrightarrow(y+z) x>y+z x$ and $(x+z) y-(x+y z)=$ $(y-1) x>0 \Longrightarrow(x+z) y>x+y z$. Therefore the only numbers that can be equal are $x+y z$ and $(y+z) x$. In this case,
$$
x+y z=(y+z) x \Longleftrightarrow(y-x)(z-x)=x(x-1)
$$
Now we can solve the items.
(a) if $n / 2<x<y<z$ then $z-x<n / 2$, and since $y-x<z-x, y-x<n / 2-1$; then
$$
(y-x)(z-x)<\frac{n}{2}\left(\frac{n}{2}-1\right)<x(x-1)
$$
and therefore $x+y z<(y+z) x$.
(b) if $x=p$, then $(y-p)(z-p)=p(p-1)$. Since $y-p<z-p,(y-p)^{2}<(y-p)(z-p)=$ $p(p-1) \Longrightarrow y-p<p$, that is, $p$ does not divide $y-p$. Then $y-p$ is a divisor $d$ of $p-1$ and $z-p=\frac{p(p-1)}{d}$. Therefore,
$$
x=p, \quad, y=p+d, \quad z=p+\frac{p(p-1)}{d}
$$
which is a solution for every divisor $d$ of $p-1$ because
$$
x=p<y=p+d<2 p \leq p+p \cdot \frac{p-1}{d}=z .
$$
Comment: If $x=1$ was allowed, then any choice $1, y, z$ would have repeated numbers in the combination, as $1 \cdot y+z=y+1 \cdot z$.
|
{
"problem_match": "# Problem 3",
"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl",
"solution_match": "# Solution\n\n"
}
| 154
| 666
|
1992
|
T1
|
4
| null |
APMO
|
Determine all pairs $(h, s)$ of positive integers with the following property: If one draws $h$ horizontal lines and another $s$ lines which satisfy
(i) they are not horizontal,
(ii) no two of them are parallel,
(iii) no three of the $h+s$ lines are concurrent,
then the number of regions formed by these $h+s$ lines is 1992 .
Answer: $(995,1),(176,10)$, and $(80,21)$.
|
Let $a_{h, s}$ the number of regions formed by $h$ horizontal lines and $s$ another lines as described in the problem. Let $\mathcal{F}_{h, s}$ be the union of the $h+s$ lines and pick any line $\ell$. If it intersects the other lines in $n$ (distinct!) points then $\ell$ is partitioned into $n-1$ line segments and 2 rays, which delimit regions. Therefore if we remove $\ell$ the number of regions decreases by exactly $n-1+2=n+1$.
Then $a_{0,0}=1$ (no lines means there is only one region), and since every one of $s$ lines intersects the other $s-1$ lines, $a_{0, s}=a_{0, s-1}+s$ for $s \geq 0$. Summing yields
$$
a_{0, s}=s+(s-1)+\cdots+1+a_{0,0}=\frac{s^{2}+s+2}{2} .
$$
Each horizontal line only intersects the $s$ non-horizontal lines, so $a_{h, s}=a_{h-1, s}+s+1$, which implies
$$
a_{h, s}=a_{0, s}+h(s+1)=\frac{s^{2}+s+2}{2}+h(s+1) .
$$
Our final task is solving
$$
a_{h, s}=1992 \Longleftrightarrow \frac{s^{2}+s+2}{2}+h(s+1)=1992 \Longleftrightarrow(s+1)(s+2 h)=2 \cdot 1991=2 \cdot 11 \cdot 181
$$
The divisors of $2 \cdot 1991$ are $1,2,11,22,181,362,1991,3982$. Since $s, h>0,2 \leq s+1<s+2 h$, so the possibilities for $s+1$ can only be 2,11 and 22 , yielding the following possibilities for $(h, s)$ :
$$
(995,1), \quad(176,10), \quad \text { and }(80,21) .
$$
|
{
"problem_match": "# Problem 4",
"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl",
"solution_match": "# Solution\n\n"
}
| 111
| 524
|
1992
|
T1
|
5
| null |
APMO
|
Find a sequence of maximal length consisting of non-zero integers in which the sum of any seven consecutive terms is positive and that of any eleven consecutive terms is negative.
Answer: The maximum length is 16 . There are several possible sequences with this length; one such sequence is $(-7,-7,18,-7,-7,-7,18,-7,-7,18,-7,-7,-7,18,-7,-7)$.
|
Suppose it is possible to have more than 16 terms in the sequence. Let $a_{1}, a_{2}, \ldots, a_{17}$ be the first 17 terms of the sequence. Consider the following array of terms in the sequence:
| $a_{1}$ | $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ |
| $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ |
| $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ |
| $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ |
| $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ | $a_{16}$ |
| $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ | $a_{16}$ | $a_{17}$ |
Let $S$ the sum of the numbers in the array. If we sum by rows we obtain negative sums in each row, so $S<0$; however, it we sum by columns we obtain positive sums in each column, so $S>0$, a contradiction. This implies that the sequence cannot have more than 16 terms. One idea to find a suitable sequence with 16 terms is considering cycles of 7 numbers. For instance, one can try
$$
-a,-a, b,-a,-a,-a, b,-a,-a, b,-a,-a,-a, b,-a,-a .
$$
The sum of every seven consecutive numbers is $-5 a+2 b$ and the sum of every eleven consecutive numbers is $-8 a+3 b$, so $-5 a+2 b>0$ and $-8 a+3 b<0$, that is,
$$
\frac{5 a}{2}<b<\frac{8 a}{3} \Longleftrightarrow 15 a<6 b<16 a
$$
Then we can choose, say, $a=7$ and $105<6 b<112 \Longleftrightarrow b=18$. A valid sequence is then
$$
-7,-7,18,-7,-7,-7,18,-7,-7,18,-7,-7,-7,18,-7,-7
$$
|
{
"problem_match": "# Problem 5",
"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl",
"solution_match": "# Solution\n\n"
}
| 94
| 913
|
1993
|
T1
|
2
| null |
APMO
|
Find the total number of different integer values the function
$$
f(x)=[x]+[2 x]+\left[\frac{5 x}{3}\right]+[3 x]+[4 x]
$$
takes for real numbers $x$ with $0 \leq x \leq 100$.
Note: $[t]$ is the largest integer that does not exceed $t$.
Answer: 734.
|
Note that, since $[x+n]=[x]+n$ for any integer $n$,
$$
f(x+3)=[x+3]+[2(x+3)]+\left[\frac{5(x+3)}{3}\right]+[3(x+3)]+[4(x+3)]=f(x)+35,
$$
one only needs to investigate the interval $[0,3)$.
The numbers in this interval at which at least one of the real numbers $x, 2 x, \frac{5 x}{3}, 3 x, 4 x$ is an integer are
- $0,1,2$ for $x$;
- $\frac{n}{2}, 0 \leq n \leq 5$ for $2 x$;
- $\frac{3 n}{5}, 0 \leq n \leq 4$ for $\frac{5 x}{3}$;
- $\frac{n}{3}, 0 \leq n \leq 8$ for $3 x$;
- $\frac{n}{4}, 0 \leq n \leq 11$ for $4 x$.
Of these numbers there are
- 3 integers $(0,1,2)$;
- 3 irreducible fractions with 2 as denominator (the numerators are $1,3,5$ );
- 6 irreducible fractions with 3 as denominator (the numerators are $1,2,4,5,7,8$ );
- 6 irreducible fractions with 4 as denominator (the numerators are $1,3,5,7,9,11,13,15$ );
- 4 irreducible fractions with 5 as denominator (the numerators are 3,6,9,12).
Therefore $f(x)$ increases 22 times per interval. Since $100=33 \cdot 3+1$, there are $33 \cdot 22$ changes of value in $[0,99)$. Finally, there are 8 more changes in [99,100]: 99, 100, $99 \frac{1}{2}, 99 \frac{1}{3}, 99 \frac{2}{3}, 99 \frac{1}{4}$, $99 \frac{3}{4}, 99 \frac{3}{5}$.
The total is then $33 \cdot 22+8=734$.
Comment: A more careful inspection shows that the range of $f$ are the numbers congruent modulo 35 to one of
$$
0,1,2,4,5,6,7,11,12,13,14,16,17,18,19,23,24,25,26,28,29,30
$$
in the interval $[0, f(100)]=[0,1166]$. Since $1166 \equiv 11(\bmod 35)$, this comprises 33 cycles plus the 8 numbers in the previous list.
|
{
"problem_match": "# Problem 2",
"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl",
"solution_match": "# Solution\n\n"
}
| 92
| 691
|
1993
|
T1
|
3
| null |
APMO
|
Let
$$
f(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{0} \quad \text { and } \quad g(x)=c_{n+1} x^{n+1}+c_{n} x^{n}+\cdots+c_{0}
$$
be non-zero polynomials with real coefficients such that $g(x)=(x+r) f(x)$ for some real number $r$. If $a=\max \left(\left|a_{n}\right|, \ldots,\left|a_{0}\right|\right)$ and $c=\max \left(\left|c_{n+1}\right|, \ldots,\left|c_{0}\right|\right)$, prove that $\frac{a}{c} \leq n+1$.
|
Expanding $(x+r) f(x)$, we find that $c_{n+1}=a_{n}, c_{k}=a_{k-1}+r a_{k}$ for $k=1,2, \ldots, n$, and $c_{0}=r a_{0}$. Consider three cases:
- $r=0$. Then $c_{0}=0$ and $c_{k}=a_{k-1}$ for $k=1,2, \ldots, n$, and $a=c \Longrightarrow \frac{a}{c}=1 \leq n+1$.
- $|r| \geq 1$. Then
$$
\begin{gathered}
\left|a_{0}\right|=\left|\frac{c_{0}}{r}\right| \leq c \\
\left|a_{1}\right|=\left|\frac{c_{1}-a_{0}}{r}\right| \leq\left|c_{1}\right|+\left|a_{0}\right| \leq 2 c
\end{gathered}
$$
and inductively if $\left|a_{k}\right| \leq(k+1) c$
$$
\left|a_{k+1}\right|=\left|\frac{c_{k+1}-a_{k}}{r}\right| \leq\left|c_{k+1}\right|+\left|a_{k}\right| \leq c+(k+1) c=(k+2) c
$$
Therefore, $\left|a_{k}\right| \leq(k+1) c \leq(n+1) c$ for all $k$, and $a \leq(n+1) c \Longleftrightarrow \frac{a}{c} \leq n+1$.
- $0<|r|<1$. Now work backwards: $\left|a_{n}\right|=\left|c_{n+1}\right| \leq c$,
$$
\left|a_{n-1}\right|=\left|c_{n}-r a_{n}\right| \leq\left|c_{n}\right|+\left|r a_{n}\right|<c+c=2 c,
$$
and inductively if $\left|a_{n-k}\right| \leq(k+1) c$
$$
\left|a_{n-k-1}\right|=\left|c_{n-k}-r a_{n-k}\right| \leq\left|c_{n-k}\right|+\left|r a_{n-k}\right|<c+(k+1) c=(k+2) c .
$$
Therefore, $\left|a_{n-k}\right| \leq(k+1) c \leq(n+1) c$ for all $k$, and $a \leq(n+1) c$ again.
|
{
"problem_match": "# Problem 3",
"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl",
"solution_match": "# Solution\n\n"
}
| 185
| 643
|
1994
|
T1
|
1
| null |
APMO
|
Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that
(i) For all $x, y \in \mathbb{R}$,
$$
f(x)+f(y)+1 \geq f(x+y) \geq f(x)+f(y)
$$
(ii) For all $x \in[0,1), f(0) \geq f(x)$,
(iii) $-f(-1)=f(1)=1$.
Find all such functions $f$.
Answer: $f(x)=\lfloor x\rfloor$, the largest integer that does not exceed $x$, is the only function.
|
Plug $y \rightarrow 1$ in (i):
$$
f(x)+f(1)+1 \geq f(x+1) \geq f(x)+f(1) \Longleftrightarrow f(x)+1 \leq f(x+1) \leq f(x)+2
$$
Now plug $y \rightarrow-1$ and $x \rightarrow x+1$ in (i):
$$
f(x+1)+f(-1)+1 \geq f(x) \geq f(x+1)+f(-1) \Longleftrightarrow f(x) \leq f(x+1) \leq f(x)+1
$$
Hence $f(x+1)=f(x)+1$ and we only need to define $f(x)$ on $[0,1)$. Note that $f(1)=$ $f(0)+1 \Longrightarrow f(0)=0$.
Condition (ii) states that $f(x) \leq 0$ in $[0,1)$.
Now plug $y \rightarrow 1-x$ in (i):
$$
f(x)+f(1-x)+1 \leq f(x+(1-x)) \leq f(x)+f(1-x) \Longrightarrow f(x)+f(1-x) \geq 0
$$
If $x \in(0,1)$ then $1-x \in(0,1)$ as well, so $f(x) \leq 0$ and $f(1-x) \leq 0$, which implies $f(x)+f(1-x) \leq 0$. Thus, $f(x)=f(1-x)=0$ for $x \in(0,1)$. This combined with $f(0)=0$ and $f(x+1)=f(x)+1$ proves that $f(x)=\lfloor x\rfloor$, which satisfies the problem conditions, as since
$x+y=\lfloor x\rfloor+\lfloor y\rfloor+\{x\}+\{y\}$ and $0 \leq\{x\}+\{y\}<2 \Longrightarrow\lfloor x\rfloor+\lfloor y\rfloor \leq x+y<\lfloor x\rfloor+\lfloor y\rfloor+2$ implies
$$
\lfloor x\rfloor+\lfloor y\rfloor+1 \geq\lfloor x+y\rfloor \geq\lfloor x\rfloor+\lfloor y\rfloor .
$$
|
{
"problem_match": "# Problem 1",
"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl",
"solution_match": "# Solution\n\n"
}
| 145
| 548
|
1994
|
T1
|
3
| null |
APMO
|
Let $n$ be an integer of the form $a^{2}+b^{2}$, where $a$ and $b$ are relatively prime integers and such that if $p$ is a prime, $p \leq \sqrt{n}$, then $p$ divides $a b$. Determine all such $n$.
Answer: $n=2,5,13$.
|
A prime $p$ divides $a b$ if and only if divides either $a$ or $b$. If $n=a^{2}+b^{2}$ is a composite then it has a prime divisor $p \leq \sqrt{n}$, and if $p$ divides $a$ it divides $b$ and vice-versa, which is not possible because $a$ and $b$ are coprime. Therefore $n$ is a prime.
Suppose without loss of generality that $a \geq b$ and consider $a-b$. Note that $a^{2}+b^{2}=(a-b)^{2}+2 a b$.
- If $a=b$ then $a=b=1$ because $a$ and $b$ are coprime. $n=2$ is a solution.
- If $a-b=1$ then $a$ and $b$ are coprime and $a^{2}+b^{2}=(a-b)^{2}+2 a b=2 a b+1=2 b(b+1)+1=$ $2 b^{2}+2 b+1$. So any prime factor of any number smaller than $\sqrt{2 b^{2}+2 b+1}$ is a divisor of $a b=b(b+1)$.
One can check that $b=1$ and $b=2$ yields the solutions $n=1^{2}+2^{2}=5$ (the only prime $p$ is 2 ) and $n=2^{2}+3^{2}=13$ (the only primes $p$ are 2 and 3 ). Suppose that $b>2$.
Consider, for instance, the prime factors of $b-1 \leq \sqrt{2 b^{2}+2 b+1}$, which is coprime with $b$. Any prime must then divide $a=b+1$. Then it divides $(b+1)-(b-1)=2$, that is, $b-1$ can only have 2 as a prime factor, that is, $b-1$ is a power of 2 , and since $b-1 \geq 2$, $b$ is odd.
Since $2 b^{2}+2 b+1-(b+2)^{2}=b^{2}-2 b-3=(b-3)(b+1) \geq 0$, we can also consider any prime divisor of $b+2$. Since $b$ is odd, $b$ and $b+2$ are also coprime, so any prime divisor of $b+2$ must divide $a=b+1$. But $b+1$ and $b+2$ are also coprime, so there can be no such primes. This is a contradiction, and $b \geq 3$ does not yield any solutions.
- If $a-b>1$, consider a prime divisor $p$ of $a-b=\sqrt{a^{2}-2 a b+b^{2}}<\sqrt{a^{2}+b^{2}}$. Since $p$ divides one of $a$ and $b, p$ divides both numbers (just add or subtract $a-b$ accordingly.) This is a contradiction.
Hence the only solutions are $n=2,5,13$.
|
{
"problem_match": "# Problem 3",
"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl",
"solution_match": "# Solution\n\n"
}
| 82
| 721
|
1994
|
T1
|
5
| null |
APMO
|
You are given three lists $A, B$, and $C$. List $A$ contains the numbers of the form $10^{k}$ in base 10, with $k$ any integer greater than or equal to 1 . Lists $B$ and $C$ contain the same numbers translated into base 2 and 5 respectively:
| $A$ | $B$ | $C$ |
| :--- | :--- | :--- |
| 10 | 1010 | 20 |
| 100 | 1100100 | 400 |
| 1000 | 1111101000 | 13000 |
| $\vdots$ | $\vdots$ | $\vdots$ |
Prove that for every integer $n>1$, there is exactly one number in exactly one of the lists $B$ or $C$ that has exactly $n$ digits.
|
Let $b_{k}$ and $c_{k}$ be the number of digits in the $k$ th term in lists $B$ and $C$, respectively. Then
$$
2^{b_{k}-1} \leq 10^{k}<2^{b_{k}} \Longleftrightarrow \log _{2} 10^{k}<b_{k} \leq \log _{2} 10^{k}+1 \Longleftrightarrow b_{k}=\left\lfloor k \cdot \log _{2} 10\right\rfloor+1
$$
and, similarly
$$
c_{k}=\left\lfloor k \cdot \log _{5} 10\right\rfloor+1
$$
Beatty's theorem states that if $\alpha$ and $\beta$ are irrational positive numbers such that
$$
\frac{1}{\alpha}+\frac{1}{\beta}=1
$$
then the sequences $\lfloor k \alpha\rfloor$ and $\lfloor k \beta\rfloor, k=1,2, \ldots$, partition the positive integers.
Then, since
$$
\frac{1}{\log _{2} 10}+\frac{1}{\log _{5} 10}=\log _{10} 2+\log _{10} 5=\log _{10}(2 \cdot 5)=1
$$
the sequences $b_{k}-1$ and $c_{k}-1$ partition the positive integers, and therefore each integer greater than 1 appears in $b_{k}$ or $c_{k}$ exactly once. We are done.
Comment: For the sake of completeness, a proof of Beatty's theorem follows.
Let $x_{n}=\alpha n$ and $y_{n}=\beta n, n \geq 1$ integer. Note that, since $\alpha m=\beta n$ implies that $\frac{\alpha}{\beta}$ is rational but
$$
\frac{\alpha}{\beta}=\alpha \cdot \frac{1}{\beta}=\alpha\left(1-\frac{1}{\alpha}\right)=\alpha-1
$$
is irrational, the sequences have no common terms, and all terms in both sequences are irrational.
The theorem is equivalent to proving that exactly one term of either $x_{n}$ of $y_{n}$ lies in the interval $(N, N+1)$ for each $N$ positive integer. For that purpose we count the number of terms of the union of the two sequences in the interval $(0, N)$ : since $n \alpha<N \Longleftrightarrow n<\frac{N}{\alpha}$, there are $\left\lfloor\frac{N}{\alpha}\right\rfloor$ terms of $x_{n}$ in the interval and, similarly, $\left\lfloor\frac{N}{\beta}\right\rfloor$ terms of $y_{n}$ in the same interval. Since the sequences are disjoint, the total of numbers is
$$
T(N)=\left\lfloor\frac{N}{\alpha}\right\rfloor+\left\lfloor\frac{N}{\beta}\right\rfloor
$$
However, $x-1<\lfloor x\rfloor<x$ for nonintegers $x$, so
$$
\begin{aligned}
\frac{N}{\alpha}-1+\frac{N}{\beta}-1<T(N)<\frac{N}{\alpha}+\frac{N}{\beta} & \Longleftrightarrow N\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)-2<T(N)<N\left(\frac{1}{\alpha}+\frac{1}{\beta}\right) \\
& \Longleftrightarrow N-2<T(N)<N,
\end{aligned}
$$
that is, $T(N)=N-1$.
Therefore the number of terms in $(N, N+1)$ is $T(N+1)-T(N)=N-(N-1)=1$, and the result follows.
|
{
"problem_match": "# Problem 5",
"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl",
"solution_match": "# Solution\n\n"
}
| 209
| 899
|
1999
|
T1
|
5
| null |
APMO
|
Let $S$ be a set of $2 n+1$ points in the plane such that no three are collinear and no four concyclic. A circle will be called good if it has 3 points of $S$ on its circumference, $n-1$ points in its interior and $n-1$ in its exterior. Prove that the number of good circles has the same parity as $n$.
|
and Marking Scheme:
Lemma 1. Let $P$ and $Q$ be two points of $S$. The number of good circles that contain $P$ and $Q$ on their circumference is odd.
## Proof of Lemma 1.
Let $N$ be the number of good circles that pass through $P$ and $Q$. Number the points on one side of the line $P Q$ by $A_{1}, A_{2}, \ldots, A_{k}$ and those on the other side by $B_{1}, B_{2}, \ldots, B_{m}$ in such a way that if $\angle P A_{i} Q=\alpha_{i}, \angle P B_{j} Q=180-\beta_{j}$ then $\alpha_{1}>\alpha_{2}>\ldots>\alpha_{k}$ and $\beta_{1}>\beta_{2}>\ldots>\beta_{m}$.
Note that the angles $\alpha_{1}, \alpha_{2}, \ldots, \alpha_{k}, \beta_{1}, \beta_{2}, \ldots, \beta_{m}$ are all distinct since there are no four points in $S$ that are concyclic.
Observe that the circle that passes through $P, Q$ and $A_{i}$ has $A_{j}$ in its interior when $\alpha_{j}>\alpha_{i}$ that is, when $i>j$; and it contains $B_{j}$ in its interior when $\alpha_{i}+180-\beta_{j}>180$, that is, when $\alpha_{i}>\beta_{j}$. Similar conditions apply to the circle that contains $P, Q$ and $B_{j}$.
1 POINT for characterizing the points that lie inside a given circle ins terms of these angles, or for similar considerations.
Order the angles $\alpha_{1}, \alpha_{2}, \ldots, \alpha_{k}, \beta_{1}, \beta_{2}, \ldots, \beta_{m}$ from the greatest to least. Now transform $S$ as follows. Consider a $\beta_{j}$ that bas an $\alpha_{i}$ immediately to its left in such an ordering ( $\ldots>\alpha_{i}>\beta_{j} \ldots$ ). Consider a new set $S^{\prime}$ that contains the same points as $S$ except for $A_{i}$ and $B_{j}$. These two points will be replaced by $A_{i}^{\prime}$ and $B_{j}^{\prime}$ that satisfy $\angle P A_{i}^{\prime} Q=\beta_{j}=\alpha_{i}^{\prime}$ and $\angle P B_{j}^{\prime} Q=180-\alpha_{i}^{\prime \prime}=180-\beta_{j}^{\prime}$. Thus $\beta_{j}$ and $\alpha_{i}$ have been interchanged and the ordering of the $\alpha$ 's and $\beta$ 's has only changed with respect to the relative order of $\alpha_{i}$ and $\beta_{j}$; we continue to have
$$
\alpha_{1}>\alpha_{2}>\ldots>\alpha_{i-1}>\alpha_{i}^{\prime}>\alpha_{i+1}>\ldots>\alpha_{k}
$$
and
$$
\beta_{1}>\beta_{2}>\ldots>\beta_{j-1}>\beta_{j}^{\prime}>\beta_{j+1}>\ldots>\beta_{m}
$$
1 POINT for this or another useful transformation of the set $S$.
Analyze the good circles in this new set $S^{\prime}$. Clearly, a circle through $P, Q, A_{r}(r \neq i)$ or through $P, Q, B_{s}(s \neq j)$ that was good in $S$ will also be good in $S^{\prime}$, because the order of $A_{r}$ (or $B_{s}$ ) relative to the rest of the points has not changed, and therefore the number of points in the interior or exterior of this circle has not changed. The only changes that could have taken place are:
a) If the circle $P, Q, A_{i}$ was good in $S$, the circle $P, Q, A_{i}^{\prime}$ may not be good in $S^{\prime}$.
b) If the circle $P, Q, B_{j}$ was good in $S$, the circle $P, Q, B_{j}^{\prime}$ may not be good in $S^{\prime}$.
c) If the circle $P, Q, A_{i}$ was not good in $S$, the circle $P, Q, A_{i}^{\prime}$ may be good in $S^{\prime}$.
d) If the circle $P, Q, B_{j}$ was not good in $S$, the circle $P, Q, B_{j}^{\prime}$ may be good in $S^{\prime}$.
1 POINT for realizing that the transformation can only change the "goodness" of these circles. But observe that the circle $P, Q, A_{i}$ contains the points $A_{1}, A_{2}, \ldots, A_{i-1}, B_{j}, B_{j+1}, \ldots, B_{m}$ and does not contain the points $A_{i+1}, A_{i+2}, \ldots, A_{k}, B_{1}, B_{2}, \ldots, B_{j-1}$ in its interior. Then this circle is good if and only if $i+m-j=k-i+j-1$, which we rewrite as $j-i=\frac{1}{2}(m-k+1)$. On the other hand, the circle $P, Q, B_{j}$ contains the points $B_{j+1}, B_{j+2}, \ldots, B_{m}, A_{1}, A_{2}, \ldots, A_{i}$ and does not contain the points $B_{1}, B_{2}, \ldots, B_{j-1}, A_{i+1}, A_{i+2}, \ldots, A_{k}$ in its interior. Hence this circle is good if and only if $m-j+i=j-1+k-i$, which we rewrite as $j-i=\frac{1}{2}(m-k+1)$.
Therefore, the circle $P, Q, A_{i}$ is good if and only if the circle $P, Q, B_{j}$ is good. Similarly, the circle $P, Q, A_{i}^{\prime}$ is good if and only if the circle $P, Q, B_{j}^{\prime}$ is good. That is to say, transforming $S$ into $S^{\prime}$ we lose either 0 or 2 good circles of $S$ and we gain either 0 or 2 good circles in $S^{\prime}$.
1 POINT for realizing that the "goodness" of these circles is changed in pairs.
Continuing in this way, we may continue to transform $S$ until we obtain a new set $S_{0}$ such that the angles $\alpha_{1}^{\prime}, \alpha_{2}^{\prime}, \ldots, \alpha_{k}^{\prime}, \beta_{1}^{\prime}, \beta_{2}^{\prime}, \ldots, \beta_{m}^{\prime}$ satisfy
$$
\beta_{1}^{\prime}>\beta_{2}^{\prime}>\ldots>\beta_{n}^{\prime}>\alpha_{1}^{\prime}>\alpha_{2}^{\prime}>\ldots>\alpha_{k}^{\prime}
$$
and such that the number of good circles in $S_{0}$ has the same parity as $N$. We claim that $S_{0}$ has exactly one good circle. In this configuration, the circle $P, Q, A_{i}$ does not contain any $B_{j}$ and the circle $P, Q, B_{r}$ does not contain any $A_{s}$ (for all $\left.i, j\right)$, because $\alpha_{a}+\left(180-\beta_{b}\right)<180$ for all $a, b$. Hence, the only possible good circles are $P, Q, B_{m-n+1}$ (which contains the $n-1$ points $B_{m-n+2}, B_{m-n+3}, \ldots, B_{m}$ ), if $m-n+1>0$, and the circle $P, Q, A_{n}$ (which contains the $n-1$ points $A_{1}, A_{2}, \ldots, A_{n}$ ), if $n \leq k$. But, since $m+k=2 n-1$, which we rewrite as $m-n+1=n-k$, exactly one of the inequalitites $m-n+1>0$ and $n \leq k$ is satisfied. It follows that one of the points $B_{m-n+1}$ and $A_{n}$ corresponds to a good circle and the other does not. Hence, $S_{0}$ has exactly one good circle, and $N$ is odd.
1 POINT for showing that this configuration has exactly one good circle.
Now consider the $\binom{2 n+1}{2}$ pairs of points in $S$. Let $a_{2 k+1}$ be the number of pairs of points through which exactly $2 k+1$ good circles pass. Then
$$
a_{1}+a_{3}+a_{5}+\ldots=\binom{2 n+1}{2}
$$
But then the number of good circles in $S$ is
$$
\begin{aligned}
\frac{1}{3}\left(a_{1}+3 a_{3}+5 a_{5}+7 a_{7}+\ldots\right) & \equiv a_{1}+3 a_{3}+5 a_{5}+7 a_{7}+\ldots \\
& \equiv a_{1}+a_{3}+a_{5}+a_{7}+\ldots \\
& \equiv\binom{2 n+1}{2} \\
& \equiv n(2 n+1) \\
& \equiv n(\bmod 2) .
\end{aligned}
$$
Here we have taken into account that each good circle is counted 3 times in the expression $a_{1}+3 a_{3}+$ $5 a_{5}+7 a_{7}+\ldots$ The desired result follows.
2 POINTS for this computation.
## Alteraative Proof of Lemma 1.
Let, $A_{1}, A_{2}, \ldots, A_{2 n-1}$ be the $2 n-1$ given points other than $P$ and $Q$.
Invert the plane with respect to point $P$. Let $O, B_{1}, B_{2}, \ldots, B_{2 n-1}$ be the images of points $Q, A_{1}, A_{2}, \ldots, A_{2 n-1}$, respectively, under this inversion. Call point $B_{i}$ "good" if the line $O B_{i}$ splits the points $B_{1}, B_{2} \ldots, B_{i-1}, B_{i+1}, \ldots, B_{2 n-1}$ evenly, leaving $n-1$ of them to each side of it. (Notice that no other $B_{j}$ can lie on the line $O B_{i}$, or else the points $P, Q, A_{i}$ and $A_{j}$ would be concyclic.) Then it is clear that the circle through $P, Q$ and $A_{i}$ is good if and only if point $B_{i}$ is good. Therefore, it suffices to prove that the number of good points is odd.
1 POINT for inverting and realizing the equivalence between good circles and good points. Notice that the good points depend only on the relative positions of rays $O B_{1}, O B_{2}, \ldots, O B_{2 n-1}$, and not on the exact positions of points $B_{1}, B_{2}, \ldots, B_{2 n-1}$. Therefore we may assume, for simplicity, that $B_{1}, B_{2}, \ldots, B_{2 n-1}$ lie on the unit circle $\Gamma$ with center $O$.
1 POINT for this or a similar simplification.
Let $C_{1}, C_{2}, \ldots, C_{2 n-1}$ be the points diametrically opposite to $B_{1}, B_{2}, \ldots, B_{2 n-1}$ in $\Gamma$. As remarked earlier, no $C_{i}$ can coincide with one of the $B_{j}$ 's. We will call the $B_{i}$ 's "white points", and the $C_{i}$ 's "black points". We will refer to these $4 n-2$ points as the "colored points".
Now we prove that the number of good points is odd, which will complete the proof of the lemma. We proceed by induction on $n$. If $n=1$, the result is trivial. Now assume that the result is true for $n=k$, and consider $2 k+1$ white points $B_{1}, B_{2}, \ldots, B_{2 k+1}$ on the circle $\Gamma$ (no two of which are diametrically opposite), and their diametrically opposite black points $C_{1}, C_{2}, \ldots, C_{2 k+1}$. Call this configuration of points "configuration 1 ". It is clear that we must have two consecutive colored points on $\Gamma$ which have different colors, say $B_{i}$ and $C_{j}$. Now remove points $B_{i}, B_{j}, C_{i}$ and $C_{j}$ from $\Gamma$, to obtain "configuration 2 ", a configuration with $2 k-1$ points of each color.
1 POINT for this or a similar transformation of the set.
It is easy to verify the following two claims:
1. Point $B_{i}$ is good in configuration 1 if and only if point $B_{j}$ is good in configuration 1.
2. Let $k \neq i, j$. Then point $B_{k}$ is good in configuration 1 if and only if it is good in configuration 2.
It follows that, by removing points $B_{i}, B_{j}, C_{i}$ and $C_{j}$, the number of good points can either stay the same, or decreases by two. In any case, its parity remains unchanged. Since we know, by the induction hypothesis, that the number of good points in configuration 2 is odd, it follows that the number of good points in configuration 1 is also odd. This completes the proof.
## Another Approach to Lemma 1.
One can give another inductive proof of lemma. 1, which combines the ideas of the two proofs that we have given. The idea is to start as in the first proof, with the characterization of the points inside a given circle.
1 POINT
Then we transform the set $S$ by removing the points $A_{i}$ and $B_{j}$ instead of replacing then by $A_{i}^{p}$ and $B_{j}^{\prime}$.
1 POINT
It can be shown that every one of the romaining circles going through $P$ and $Q$, contained exactly one of $A_{i}$ and $B_{j}$. Therefore, the only good circles we could have gained or lost are $P, Q, A_{i}$ and $P, Q, B_{j}$.
2 POINTS
Finally, we show that either both or none of these circles were good, so the parity of the number of good circles isn't changed by this transformation.
1 POINT
Remark: 2 POINTS can be given if the result has been fully proved for a particular case with $n>1$. (If more than one particular case has been analyzed completly, only 2 POINTS.) These points are awarded only if no progress has been made in the general solution of the problem.
|
{
"problem_match": "\nProblem 5.",
"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl",
"solution_match": "# Solution "
}
| 86
| 3,594
|
2000
|
T1
|
2
| null |
APMO
|
Given the following arrangement of circles:
Each of the numbers $1,2, \ldots, 9$ is to be written into one of these circles, so that each circle contains exactly one of these numbers and
(i) the sums of the four numbers on each side of the triangle are equal;
(ii) the sums of squares of the four numbers on each side of the triangle are equal.
Find all ways in which this can be done.
Answer: The only solutions are
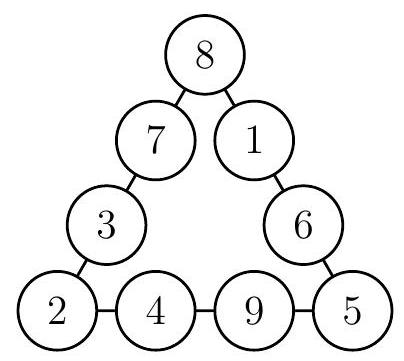
and the ones generated by permuting the vertices, adjusting sides and exchanging the two middle numbers on each side.
|
Let $a, b$, and $c$ be the numbers in the vertices of the triangular arrangement. Let $s$ be the sum of the numbers on each side and $t$ be the sum of the squares of the numbers on each side. Summing the numbers (or their squares) on the three sides repeats each once the numbers on the vertices (or their squares):
$$
\begin{gathered}
3 s=a+b+c+(1+2+\cdots+9)=a+b+c+45 \\
3 t=a^{2}+b^{2}+c^{2}+\left(1^{2}+2^{2}+\cdots+9^{2}\right)=a^{2}+b^{2}+c^{2}+285
\end{gathered}
$$
At any rate, $a+b+c$ and $a^{2}+b^{2}+c^{2}$ are both multiples of 3 . Since $x^{2} \equiv 0,1(\bmod 3)$, either $a, b, c$ are all multiples of 3 or none is a multiple of 3 . If two of them are $1,2 \bmod 3$ then $a+b+c \equiv 0(\bmod 3)$ implies that the other should be a multiple of 3 , which is not possible. Thus $a, b, c$ are all congruent modulo 3 , that is,
$$
\{a, b, c\}=\{3,6,9\}, \quad\{1,4,7\}, \quad \text { or } \quad\{2,5,8\}
$$
Case 1: $\{a, b, c\}=\{3,6,9\}$. Then $3 t=3^{2}+6^{2}+9^{2}+285 \Longleftrightarrow t=137$.
In this case $x^{2}+y^{2}+3^{2}+9^{2}=137 \Longleftrightarrow x^{2}+y^{2}=47$. However, 47 cannot be written as the sum of two squares. One can check manually, or realize that $47 \equiv 3(\bmod 4)$, and since $x^{2}, y^{2} \equiv 0,1(\bmod 4), x^{2}+y^{2} \equiv 0,1,2(\bmod 4)$ cannot be 47.
Hence there are no solutions in this case.
Case 2: $\{a, b, c\}=\{1,4,7\}$. Then $3 t=1^{2}+4^{2}+7^{2}+285 \Longleftrightarrow t=117$.
In this case $x^{2}+y^{2}+1^{2}+7^{2}=117 \Longleftrightarrow x^{2}+y^{2}=67 \equiv 3(\bmod 4)$, and as in the previous case there are no solutions.
Case 3: $\{a, b, c\}=\{2,5,8\}$. Then $3 t=2^{2}+5^{2}+8^{2}+285 \Longleftrightarrow t=126$.
Then
$$
\left\{\begin{array} { c }
{ x ^ { 2 } + y ^ { 2 } + 2 ^ { 2 } + 8 ^ { 2 } = 1 2 6 } \\
{ t ^ { 2 } + u ^ { 2 } + 2 ^ { 2 } + 5 ^ { 2 } = 1 2 6 } \\
{ m ^ { 2 } + n ^ { 2 } + 5 ^ { 2 } + 8 ^ { 2 } = 1 2 6 }
\end{array} \Longleftrightarrow \left\{\begin{array}{c}
x^{2}+y^{2}=58 \\
t^{2}+u^{2}=97 \\
m^{2}+n^{2}=37
\end{array}\right.\right.
$$
The only solutions to $t^{2}+u^{2}=97$ and $m^{2}+n^{2}=37$ are $\{t, u\}=\{4,9\}$ and $\{m, n\}=\{1,6\}$, respectively (again, one can check manually.) Then $\{x, y\}=\{3,7\}$, and the solutions are
and the ones generated by permuting the vertices, adjusting sides and exchanging the two middle numbers on each side. There are $3!\cdot 2^{3}=48$ such solutions.
|
{
"problem_match": "# Problem 2",
"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl",
"solution_match": "# Solution\n\n"
}
| 264
| 1,062
|
2000
|
T1
|
3
| null |
APMO
|
Let $A B C$ be a triangle. Let $M$ and $N$ be the points in which the median and angle bisector, respectively, at $A$ meet the side $B C$. Let $Q$ and $P$ be the points in which the perpendicular at $N$ to $N A$ meets $M A$ and $B A$, respectively, and $O$ be the point in which the perpendicular at $P$ to $B A$ meets $A N$ produced. Prove that $Q O$ is perpendicular to $B C$.
|
Consider a cartesian plane with $A=(0,0)$ as the origin and the bisector $A N$ as $x$-axis. Thus $A B$ has equation $y=m x$ and $A C$ has equation $y=-m x$. Let $B=(b, m b)$ and $C=(c,-m c)$. By symmetry, the problem is immediate if $A B=A C$, that is, if $b=c$. Suppose that $b \neq c$ from now on. Line $B C$ has slope $\frac{m b-(-m c)}{b-c}=\frac{m(b+c)}{b-c}$. Let $N=(n, 0)$.
Point $M$ is the midpoint $\left(\frac{b+c}{2}, \frac{m b-m c}{2}\right)$ of $B C$, so $A M$ has slope $\frac{m(b-c)}{b+c}$.
The line through $N$ that is perpendicular to the $x$-axis $A N$ is $x=n$. Therefore
$$
P=(n, m n) \quad \text { and } \quad Q=\left(n, \frac{m(b-c) n}{b+c}\right) .
$$
In the right triangle $A P O$, with altitude $A N, A N \cdot A O=A P^{2}$. Thus
$$
n \cdot A O=(0-n)^{2}+(0-m n)^{2} \Longleftrightarrow A O=n\left(m^{2}+1\right) \Longrightarrow O=\left(n\left(m^{2}+1\right), 0\right)
$$
Finally, the slope of $O Q$ is
$$
\frac{\frac{m(b-c) n}{b+c}-0}{n-n\left(m^{2}+1\right)}=-\frac{b-c}{(b+c) m}
$$
Since the product of the slopes of $O Q$ and $B C$ is
$$
-\frac{b-c}{(b+c) m} \cdot \frac{m(b+c)}{b-c}=-1
$$
$O Q$ and $B C$ are perpendicular, and we are done.
Comment: The second solution shows that $N$ can be any point in the bisector of $\angle A$. In fact, if we move $N$ in the bisector and construct $O, P$ and $Q$ accordingly, then all lines $O Q$ obtained are parallel: just consider a homothety with center $A$ and variable ratios.
|
{
"problem_match": "# Problem 3",
"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl",
"solution_match": "# Solution 2"
}
| 120
| 563
|
2000
|
T1
|
4
| null |
APMO
|
Let $n, k$ be given positive integers with $n>k$. Prove that
$$
\frac{1}{n+1} \cdot \frac{n^{n}}{k^{k}(n-k)^{n-k}}<\frac{n!}{k!(n-k)!}<\frac{n^{n}}{k^{k}(n-k)^{n-k}} .
$$
|
The inequality is equivalent to
$$
\frac{n^{n}}{n+1}<\binom{n}{k} k^{k}(n-k)^{n-k}<n^{n}
$$
which suggests investigating the binomial expansion of
$$
n^{n}=((n-k)+k)^{n}=\sum_{i=0}^{n}\binom{n}{i}(n-k)^{n-i} k^{i}
$$
The $(k+1)$ th term $T_{k+1}$ of the expansion is $\binom{n}{k} k^{k}(n-k)^{n-k}$, and all terms in the expansion are positive, which implies the right inequality.
Now, for $1 \leq i \leq n$,
$$
\frac{T_{i+1}}{T_{i}}=\frac{\binom{n}{i}(n-k)^{n-i} k^{i}}{\binom{n}{i-1}(n-k)^{n-i+1} k^{i-1}}=\frac{(n-i+1) k}{i(n-k)}
$$
and
$$
\frac{T_{i+1}}{T_{i}}>1 \Longleftrightarrow(n-i+1) k>i(n-k) \Longleftrightarrow i<k+\frac{k}{n} \Longleftrightarrow i \leq k
$$
This means that
$$
T_{1}<T_{2}<\cdots<T_{k+1}>T_{k+2}>\cdots>T_{n+1}
$$
that is, $T_{k+1}=\binom{n}{k} k^{k}(n-k)^{n-k}$ is the largest term in the expansion. The maximum term is greater that the average, which is the sum $n^{n}$ divided by the quantity $n+1$, therefore
$$
\binom{n}{k} k^{k}(n-k)^{n-k}>\frac{n^{n}}{n+1}
$$
as required.
Comment: If we divide further by $n^{n}$ one finds
$$
\frac{1}{n+1}<\binom{n}{k}\left(\frac{k}{n}\right)^{k}\left(1-\frac{k}{n}\right)^{n-k}<1
$$
The middle term is the probability $P(X=k)$ of $k$ successes in a binomial distribution with $n$ trials and success probability $p=\frac{k}{n}$. The right inequality is immediate from the fact that $P(X=k)$ is not the only possible event in this distribution, and the left inequality comes from the fact that the mode of the binomial distribution are given by $\lfloor(n+1) p\rfloor=\left\lfloor(n+1) \frac{k}{n}\right\rfloor=k$ and $\lceil(n+1) p-1\rceil=k$. However, the proof of this fact is identical to the above solution.
|
{
"problem_match": "# Problem 4",
"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl",
"solution_match": "# Solution\n\n"
}
| 82
| 639
|
2000
|
T1
|
5
| null |
APMO
|
Given a permutation $\left(a_{0}, a_{1}, \ldots, a_{n}\right)$ of the sequence $0,1, \ldots, n$. A transposition of $a_{i}$ with $a_{j}$ is called legal if $a_{i}=0$ for $i>0$, and $a_{i-1}+1=a_{j}$. The permutation $\left(a_{0}, a_{1}, \ldots, a_{n}\right)$ is called regular if after a number of legal transpositions it becomes $(1,2, \ldots, n, 0)$. For which numbers $n$ is the permutation $(1, n, n-1, \ldots, 3,2,0)$ regular?
Answer: $n=2$ and $n=2^{k}-1, k$ positive integer.
|
A legal transposition consists of looking at the number immediately before 0 and exchanging 0 and its successor; therefore, we can perform at most one legal transposition to any permutation, and a legal transposition is not possible only and if only 0 is preceded by $n$.
If $n=1$ or $n=2$ there is nothing to do, so $n=1=2^{1}-1$ and $n=2$ are solutions. Suppose that $n>3$ in the following.
Call a pass a maximal sequence of legal transpositions that move 0 to the left. We first illustrate what happens in the case $n=15$, which is large enough to visualize what is going on. The first pass is
$$
\begin{aligned}
& (1,15,14,13,12,11,10,9,8,7,6,5,4,3,2,0) \\
& (1,15,14,13,12,11,10,9,8,7,6,5,4,0,2,3) \\
& (1,15,14,13,12,11,10,9,8,7,6,0,4,5,2,3) \\
& (1,15,14,13,12,11,10,9,8,0,6,7,4,5,2,3) \\
& (1,15,14,13,12,11,10,0,8,9,6,7,4,5,2,3) \\
& (1,15,14,13,12,0,10,11,8,9,6,7,4,5,2,3) \\
& (1,15,14,0,12,13,10,11,8,9,6,7,4,5,2,3) \\
& (1,0,14,15,12,13,10,11,8,9,6,7,4,5,2,3)
\end{aligned}
$$
After exchanging 0 and 2, the second pass is
$$
\begin{aligned}
& (1,2,14,15,12,13,10,11,8,9,6,7,4,5,0,3) \\
& (1,2,14,15,12,13, \mathbf{1 0}, 11,8,9,0,7,4,5,6,3) \\
& (1,2, \mathbf{1 4}, 15,12,13,0,11,8,9,10,7,4,5,6,3) \\
& (1,2,0,15,12,13,14,11,8,9,10,7,4,5,6,3)
\end{aligned}
$$
After exchanging 0 and 3 , the third pass is
$$
\begin{aligned}
& (1,2,3,15,12,13,14,11,8,9,10,7,4,5,6,0) \\
& (1,2,3,15,12,13,14,11,8,9,10,0,4,5,6,7) \\
& (1,2,3,15,12,13,14,0,8,9,10,11,4,5,6,7) \\
& (1,2,3,0,12,13,14,15,8,9,10,11,4,5,6,7)
\end{aligned}
$$
After exchanging 0 and 4, the fourth pass is
$$
\begin{aligned}
& (1,2,3,4,12,13,14,15,8,9,10,11,0,5,6,7) \\
& (1,2,3,4,0,13,14,15,8,9,10,11,12,5,6,7)
\end{aligned}
$$
And then one can successively perform the operations to eventually find
$$
(1,2,3,4,5,6,7,0,8,9,10,11,12,13,14,15)
$$
after which 0 will move one unit to the right with each transposition, and $n=15$ is a solution. The general case follows.
Case 1: $n>2$ even: After the first pass, in which 0 is transposed successively with $3,5, \ldots, n-1$, after which 0 is right after $n$, and no other legal transposition can be performed. So $n$ is not a solution in this case.
Case 2: $n=2^{k}-1$ : Denote $N=n+1, R=2^{r},[a: b]=(a, a+1, a+2, \ldots, b)$, and concatenation by a comma. Let $P_{r}$ be the permutation
$$
[1: R-1],(0),[N-R: N-1],[N-2 R: N-R-1], \ldots,[2 R: 3 R-1],[R: 2 R-1]
$$
$P_{r}$ is formed by the blocks $[1: R-1],(0)$, and other $2^{k-r}-1$ blocks of size $R=2^{r}$ with consecutive numbers, beginning with $t R$ and finishing with $(t+1) R-1$, in decreasing order of $t$. Also define $P_{0}$ as the initial permutation.
Then it can be verified that $P_{r+1}$ is obtained from $P_{r}$ after a number of legal transpositions: it can be easily verified that $P_{0}$ leads to $P_{1}$, as 0 is transposed successively with $3,5, \ldots, n-1$, shifting cyclically all numbers with even indices; this is $P_{1}$.
Starting from $P_{r}, r>0$, 0 is successively transposed with $R, 3 R, \ldots, N-R$. The numbers $0, N-R, N-3 R, \ldots, 3 R, R$ are cyclically shifted. This means that $R$ precedes 0 , and the blocks become
$$
\begin{gathered}
{[1: R],(0),[N-R+1: N-1],[N-2 R: N-R],[N-3 R+1: N-2 R-1], \ldots,} \\
{[3 R+1: 4 R-1],[2 R: 3 R],[R+1: 2 R-1]}
\end{gathered}
$$
Note that the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number.
Now $0, N-R+1, N-3 R+1, \ldots, 3 R+1, R+1$ are shifted. Note that, for every $i$ th block, $i$ odd greater than 1 , the first number is cyclically shifted, and the blocks become
$$
\begin{gathered}
{[1: R+1],(0),[N-R+2: N-1],[N-2 R: N-R+1],[N-3 R+2: N-2 R-1], \ldots,} \\
{[3 R+1: 4 R-1],[2 R: 3 R+1],[R+2: 2 R-1]}
\end{gathered}
$$
The same phenomenom happened: the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number. This pattern continues: $0, N-R+u, N-3 R+u, \ldots, R+u$ are shifted, $u=0,1,2, \ldots, R-1$, the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number, until they vanish. We finish with
$$
[1: 2 R-1],(0),[N-2 R: N-1], \ldots,[2 R: 4 R-1]
$$
which is precisely $P_{r+1}$.
Since $P_{k}=[1: N-1],(0), n=2^{k}-1$ is a solution.
Case 3: $n$ is odd, but is not of the form $2^{k}-1$. Write $n+1$ as $n+1=2^{a}(2 b+1), b \geq 1$, and define $P_{0}, \ldots, P_{a}$ as in the previous case. Since $2^{a}$ divides $N=n+1$, the same rules apply, and we obtain $P_{a}$ :
$$
\left[1: 2^{a}-1\right],(0),\left[N-2^{a}: N-1\right],\left[N-2^{a+1}: N-2^{a}-1\right], \ldots,\left[2^{a+1}: 3 \cdot 2^{a}-1\right],\left[2^{a}: 2^{a+1}-1\right]
$$
But then 0 is transposed with $2^{a}, 3 \cdot 2^{a}, \ldots,(2 b-1) \cdot 2^{a}=N-2^{a+1}$, after which 0 is put immediately after $N-1=n$, and cannot be transposed again. Therefore, $n$ is not a solution. All cases were studied, and so we are done.
Comment: The general problem of finding the number of regular permutations for any $n$ seems to be difficult. A computer finds the first few values
$$
1,2,5,14,47,189,891,4815,29547
$$
which is not catalogued at oeis.org.
|
{
"problem_match": "# Problem 5",
"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl",
"solution_match": "# Solution\n\n"
}
| 187
| 2,361
|
2002
|
T1
|
1
| null |
APMO
|
Let $a_{1}, a_{2}, a_{3}, \ldots, a_{n}$ be a sequence of non-negative integers, where $n$ is a positive integer.
Let
$$
A_{n}=\frac{a_{1}+a_{2}+\cdots+a_{n}}{n}
$$
Prove that
$$
a_{1}!a_{2}!\ldots a_{n}!\geq\left(\left\lfloor A_{n}\right\rfloor!\right)^{n}
$$
where $\left\lfloor A_{n}\right\rfloor$ is the greatest integer less than or equal to $A_{n}$, and $a!=1 \times 2 \times \cdots \times a$ for $a \geq 1$ (and $0!=1$ ). When does equality hold?
|
Assume without loss of generality that $a_{1} \geq a_{2} \geq \cdots \geq a_{n} \geq 0$, and let $s=\left\lfloor A_{n}\right\rfloor$. Let $k$ be any (fixed) index for which $a_{k} \geq s \geq a_{k+1}$.
Our inequality is equivalent to proving that
$$
\frac{a_{1}!}{s!} \cdot \frac{a_{2}!}{s!} \cdot \ldots \cdot \frac{a_{k}!}{s!} \geq \frac{s!}{a_{k+1}!} \cdot \frac{s!}{a_{k+2}!} \cdot \ldots \cdot \frac{s!}{a_{n}!}
$$
Now for $i=1,2, \ldots, k, a_{i}!/ s!$ is the product of $a_{i}-s$ factors. For example, 9!/5! $=9 \cdot 8 \cdot 7 \cdot 6$. The left side of inequality (1) therefore is the product of $A=a_{1}+a_{2}+\cdots+a_{k}-k s$ factors, all of which are greater than $s$. Similarly, the right side of (1) is the product of $B=(n-k) s-$ $\left(a_{k+1}+a_{k+2}+\cdots+a_{n}\right)$ factors, all of which are at most $s$. Since $\sum_{i=1}^{n} a_{i}=n A_{n} \geq n s, A \geq B$. This proves the inequality. [ 5 marks to here.]
Equality in (1) holds if and only if either:
(i) $A=B=0$, that is, both sides of (1) are the empty product, which occurs if and only if $a_{1}=a_{2}=\cdots=a_{n}$; or
(ii) $a_{1}=1$ and $s=0$, that is, the only factors on either side of (1) are 1 's, which occurs if and only if $a_{i} \in\{0,1\}$ for all $i$. [2 marks for both (i) and (ii), no marks for (i) only.]
|
{
"problem_match": "\n1. ",
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"solution_match": "# Solution 1."
}
| 189
| 537
|
2002
|
T1
|
1
| null |
APMO
|
Let $a_{1}, a_{2}, a_{3}, \ldots, a_{n}$ be a sequence of non-negative integers, where $n$ is a positive integer.
Let
$$
A_{n}=\frac{a_{1}+a_{2}+\cdots+a_{n}}{n}
$$
Prove that
$$
a_{1}!a_{2}!\ldots a_{n}!\geq\left(\left\lfloor A_{n}\right\rfloor!\right)^{n}
$$
where $\left\lfloor A_{n}\right\rfloor$ is the greatest integer less than or equal to $A_{n}$, and $a!=1 \times 2 \times \cdots \times a$ for $a \geq 1$ (and $0!=1$ ). When does equality hold?
|
Assume without loss of generality that $0 \leq a_{1} \leq a_{2} \leq \cdots \leq a_{n}$. Let $d=a_{n}-a_{1}$ and $m=\left|\left\{i: a_{i}=a_{1}\right\}\right|$. Our proof is by induction on $d$.
We first do the case $d=a_{n}-a_{1}=0$ or 1 separately. Then $a_{1}=a_{2}=\cdots=a_{m}=a$ and $a_{m+1}=\cdots=a_{n}=a+1$ for some $1 \leq m \leq n$ and $a \geq 0$. In this case we have $\left\lfloor A_{n}\right\rfloor=a$, so the inequality to be proven is just $a_{1}!a_{2}!\ldots a_{n}!\geq(a!)^{n}$, which is obvious. Equality holds if and only if either $m=n$, that is, $a_{1}=a_{2}=\cdots=a_{n}=a$; or if $a=0$, that is, $a_{1}=\cdots=a_{m}=0$ and $a_{m+1}=\cdots=a_{n}=1$. [ 2 marks to here.]
So assume that $d=a_{n}-a_{1} \geq 2$ and that the inequality holds for all sequences with smaller values of $d$, or with the same value of $d$ and smaller values of $m$. Then the sequence
$$
a_{1}+1, a_{2}, a_{3}, \ldots, a_{n-1}, a_{n}-1
$$
though not necessarily in non-decreasing order any more, does have either a smaller value of $d$, or the same value of $d$ and a smaller value of $m$, but in any case has the same value of $A_{n}$. Thus, by induction and since $a_{n}>a_{1}+1$,
$$
\begin{aligned}
a_{1}!a_{2}!\ldots a_{n}! & =\left(a_{1}+1\right)!a_{2}!\ldots a_{n-1}!\left(a_{n}-1\right)!\cdot \frac{a_{n}}{a_{1}+1} \\
& \geq\left(\left\lfloor A_{n}\right\rfloor!\right)^{n} \cdot \frac{a_{n}}{a_{1}+1} \\
& >\left(\left\lfloor A_{n}\right\rfloor!\right)^{n}
\end{aligned}
$$
which completes the proof. Equality cannot hold in this case.
|
{
"problem_match": "\n1. ",
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"solution_match": "\nSolution 2."
}
| 189
| 628
|
2002
|
T1
|
2
| null |
APMO
|
Find all positive integers $a$ and $b$ such that
$$
\frac{a^{2}+b}{b^{2}-a} \text { and } \frac{b^{2}+a}{a^{2}-b}
$$
are both integers.
|
By the symmetry of the problem, we may suppose that $a \leq b$. Notice that $b^{2}-a \geq 0$, so that if $\frac{a^{2}+b}{b^{2}-a}$ is a positive integer, then $a^{2}+b \geq b^{2}-a$. Rearranging this inequality and factorizing, we find that $(a+b)(a-b+1) \geq 0$. Since $a, b>0$, we must have $a \geq b-1$. [3 marks to here.] We therefore have two cases:
Case 1: $a=b$. Substituting, we have
$$
\frac{a^{2}+a}{a^{2}-a}=\frac{a+1}{a-1}=1+\frac{2}{a-1},
$$
which is an integer if and only if $(a-1) \mid 2$. As $a>0$, the only possible values are $a-1=1$ or 2. Hence, $(a, b)=(2,2)$ or $(3,3)$. [1 mark.]
Case 2: $a=b-1$. Substituting, we have
$$
\frac{b^{2}+a}{a^{2}-b}=\frac{(a+1)^{2}+a}{a^{2}-(a+1)}=\frac{a^{2}+3 a+1}{a^{2}-a-1}=1+\frac{4 a+2}{a^{2}-a-1} .
$$
Once again, notice that $4 a+2>0$, and hence, for $\frac{4 a+2}{a^{2}-a-1}$ to be an integer, we must have $4 a+2 \geq a^{2}-a-1$, that is, $a^{2}-5 a-3 \leq 0$. Hence, since $a$ is an integer, we can bound $a$ by $1 \leq \bar{a} \leq 5$. Checking all the ordered pairs $(a, b)=(1,2),(2,3), \ldots,(5,6)$, we find that only $(1,2)$ and $(2,3)$ satisfy the given conditions. [3 marks.]
Thus, the ordered pairs that work are
$$
(2,2),(3,3),(1,2),(2,3),(2,1),(3,2)
$$
where the last two pairs follow by symmetry. [2 marks if these solutions are found without proof that there are no others.]
|
{
"problem_match": "\n2. ",
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"solution_match": "\nSolution."
}
| 59
| 570
|
2002
|
T1
|
3
| null |
APMO
|
Let $A B C$ be an equilateral triangle. Let $P$ be a point on the side $A C$ and $Q$ be a point on the side $A B$ so that both triangles $A B P$ and $A C Q$ are acute. Let $R$ be the orthocentre of triangle $A B P$ and $S$ be the orthocentre of triangle $A C Q$. Let $T$ be the point common to the segments $B P$ and $C Q$. Find all possible values of $\angle C B P$ and $\angle B C Q$ such that triangle $T R S$ is equilateral.
|
We are going to show that this can only happen when
$$
\angle C B P=\angle B C Q=15^{\circ} .
$$
Lemma. If $\angle C B P>\angle B C Q$, then $R T>S T$.
Proof. Let $A D, B E$ and $C F$ be the altitudes of triangle $A B C$ concurrent at its centre $G$. Then $P$ lies on $C E, Q$ lies on $B F$, and thus $T$ lies in triangle $B D G$.
Note that -
$$
\angle F A S=\angle F C Q=30^{\circ}-\angle B C Q>30^{\circ}-\angle C B P=\angle E B P=\angle E A R
$$
Since $A F=A E$, we have $F S>E R$ so that
$$
G S=G F-F S<G E-E R=G R .
$$
Let $T_{x}$ be the projection of $T$ onto $B C$ and $T_{y}$ be the projection of $T$ onto $A D$, and similarly for $R$ and $S$. We have
$$
R_{x} T_{x}=D R_{x}+D T_{x}>\left|D S_{x}-D T_{x}\right|=S_{x} T_{x}
$$
and
$$
R_{y} T_{y}=G R_{y}+G T_{y}>G S_{y}+G T_{y}=S_{y} T_{y}
$$
It follows that $R T>S T$.
[1 mark for stating the Lemma, 3 marks for proving it.]
Thus, if $\triangle T R S$ is equilateral, we must have $\angle C B P=\angle B C Q$.
It is clear from the symmetry of the figure that $T R=T S$, so $\triangle T R S$ is equilateral if and only if $\angle R T A=30^{\circ}$. Now, as $B R$ is an altitude of the triangle $A B C, \angle R B A=30^{\circ}$. So $\triangle T R S$ is equilateral if and only if $R T B A$ is a cyclic quadrilateral. Therefore, $\triangle T R S$ is equilateral if and only if $\angle T B R=\angle T A R$. But
$$
\begin{aligned}
90^{\circ} & =\angle T B A+\angle B A R \\
& =(\angle T B R+\angle R B A)+(\angle B A T+\angle T A R) \\
& =\left(\angle T B R+30^{\circ}\right)+\left(30^{\circ}+\angle T A R\right)
\end{aligned}
$$
and so
$$
30^{\circ}=\angle T A R+\angle T B R
$$
But these angles must be equal, so $\angle T A R=\angle T B R=15^{\circ}$. Therefore $\angle C B P=\angle B C Q=15^{\circ}$. [3 marks for finishing the proof with the assumption that $\angle C B P=\angle B C Q$.]
|
{
"problem_match": "\n3. ",
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"solution_match": "# Solution."
}
| 140
| 714
|
2002
|
T1
|
4
| null |
APMO
|
Let $x, y, z$ be positive numbers such that
$$
\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1
$$
Show that
$$
\sqrt{x+y z}+\sqrt{y+z x}+\sqrt{z+x y} \geq \sqrt{x y z}+\sqrt{x}+\sqrt{y}+\sqrt{z}
$$
|
This is another way of presenting the idea in the first solution.
Using the condition $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1$ and the AM-GM inequality, we have
$$
\begin{aligned}
x+y z-\left(\sqrt{\frac{y z}{x}}+\sqrt{x}\right)^{2} & =y z\left(1-\frac{1}{x}\right)-2 \sqrt{y z} \\
& =y z\left(\frac{1}{y}+\frac{1}{z}\right)-2 \sqrt{y z}=y+z-2 \sqrt{y z} \geq 0
\end{aligned}
$$
which gives
$$
\sqrt{x+y z} \geq \sqrt{\frac{y z}{x}}+\sqrt{x} . \quad[3 \text { marks. }]
$$
Similarly, we have
$$
\sqrt{y+z x} \geq \sqrt{\frac{z x}{y}}+\sqrt{y} \text { and } \sqrt{z+x y} \geq \sqrt{\frac{x y}{z}}+\sqrt{z}
$$
Addition yields
$$
\sqrt{x+y z}+\sqrt{y+z x}+\sqrt{z+x y} \geq \sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}+\sqrt{x}+\sqrt{y}+\sqrt{z}
$$
[2 marks.] Using the condition $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1$ again, we have
$$
\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}=\sqrt{x y z}\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)=\sqrt{x y z}, \quad[1 \text { mark. }]
$$
and thus
$$
\sqrt{x+y z}+\sqrt{y+z x}+\sqrt{z+x y} \geq \sqrt{x y z}+\sqrt{x}+\sqrt{y}+\sqrt{z} . \quad[1 \text { mark. }]
$$
|
{
"problem_match": "\n4. ",
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"solution_match": "\nSolution 3."
}
| 90
| 509
|
2002
|
T1
|
4
| null |
APMO
|
Let $x, y, z$ be positive numbers such that
$$
\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1
$$
Show that
$$
\sqrt{x+y z}+\sqrt{y+z x}+\sqrt{z+x y} \geq \sqrt{x y z}+\sqrt{x}+\sqrt{y}+\sqrt{z}
$$
|
This is also another way of presenting the idea in the first solution.
We make the substitution $a=\frac{1}{x}, b=\frac{1}{y}, c=\frac{1}{z}$. Then it is enough to show that
$$
\sqrt{\frac{1}{a}+\frac{1}{b c}}+\sqrt{\frac{1}{b}+\frac{1}{c a}}+\sqrt{\frac{1}{c}+\frac{1}{a b}} \geq \sqrt{\frac{1}{a b c}}+\sqrt{\frac{1}{a}}+\sqrt{\frac{1}{b}}+\sqrt{\frac{1}{c}},
$$
where $a+b+c=1$. Multiplying this inequality by $\sqrt{a b c}$, we find that it can be written
$$
\sqrt{a+b c}+\sqrt{b+c a}+\sqrt{c+a b} \geq 1+\sqrt{b c}+\sqrt{c a}+\sqrt{a b} . \quad[1 \text { mark. }]
$$
This is equivalent to
$$
\begin{aligned}
& \sqrt{a(a+b+c)+b c}+\sqrt{b(a+b+c)+c a}+\sqrt{c(a+b+c)+a b} \\
& \geq a+b+c+\sqrt{b c}+\sqrt{c a}+\sqrt{a b}, \quad[1 \text { mark. }]
\end{aligned}
$$
which in turn is equivalent to
$$
\sqrt{(a+b)(a+c)}+\sqrt{(b+c)(b+a)}+\sqrt{(c+a)(c+b)} \geq a+b+c+\sqrt{b c}+\sqrt{c a}+\sqrt{a b}
$$
[1 mark.] (This is a homogeneous version of the original inequality.) By the Cauchy-Schwarz inequality (or since $b+c \geq 2 \sqrt{b c}$ ), we have
$$
\left[(\sqrt{a})^{2}+(\sqrt{b})^{2}\right]\left[(\sqrt{a})^{2}+(\sqrt{c})^{2}\right] \geq(\sqrt{a} \sqrt{a}+\sqrt{b} \sqrt{c})^{2}
$$
or
$$
\sqrt{(a+b)(a+c)} \geq a+\sqrt{b c} . \quad[2 \text { marks. }]
$$
Taking the cyclic sum of this inequality over $a, b, c$, we get the desired inequality. [2 marks.]
|
{
"problem_match": "\n4. ",
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"solution_match": "# Solution 4."
}
| 90
| 564
|
2002
|
T1
|
5
| null |
APMO
|
Let R denote the set of all real numbers. Find all functions $f$ from R to R satisfying:
(i) there are only finitely many $s$ in R such that $f(s)=0$, and
(ii) $f\left(x^{4}+y\right)=x^{3} f(x)+f(f(y))$ for all $x, y$ in $\mathbf{R}$.
|
The only such function is the identity function on $R$.
Setting $(x, y)=(1,0)$ in the given functional equation (ii), we have $f(f(0))=0$. Setting $x=0$ in (ii), we find
$$
f(y)=f(f(y))
$$
[1 mark.] and thus $f(0)=f(f(0))=0$ [1 mark.]. It follows from (ii) that $f\left(x^{4}+y\right)=$ $x^{3} f(x)+f(y)$ for all $x, y \in \mathbf{R}$. Set $y=0$ to obtain
$$
f\left(x^{4}\right)=x^{3} f(x)
$$
for all $x \in \mathrm{R}$, and so
$$
f\left(x^{4}+y\right)=f\left(x^{4}\right)+f(y)
$$
for all $x, y \in \mathbf{R}$. The functional equation (3) suggests that $f$ is additive, that is, $f(a+b)=$ $f(a)+f(b)$ for all $a, b \in \mathbf{R}$. [1 mark.] We now show this.
First assume that $a \geq 0$ and $b \in R$. It follows from (3) that
$$
f(a+b)=f\left(\left(a^{1 / 4}\right)^{4}+b\right)=f\left(\left(a^{1 / 4}\right)^{4}\right)+f(b)=f(a)+f(b)
$$
We next note that $f$ is an odd function, since from (2)
$$
f(-x)=\frac{f\left(x^{4}\right)}{(-x)^{3}}=\frac{f\left(x^{4}\right)}{-x^{3}}=-f(x), \quad x \neq 0
$$
Since $f$ is odd, we have that, for $a<0$ and $b \in R$,
$$
\begin{aligned}
f(a+b) & =-f((-a)+(-b))=-(f(-a)+f(-b)) \\
& =-(-f(a)-f(b))=f(a)+f(b)
\end{aligned}
$$
Therefore, we conclude that $f(a+b)=f(a)+f(b)$ for all $a, b \in R$. [2 mers.].]
We now show that $\{s \in \mathrm{R} \mid f(s)=0\}=\{0\}$. Recall that $f(0)=0$. Assume that there is a nonzero $h \in \mathrm{R}$ such that $f(h)=0$. Then, using the fact that $f$ is additive, we inductively have $f(n h)=0$ or $n h \in\{s \in R \mid f(s)=0\}$ for all $n \in \mathbf{N}$. However, this is a contradiction to the given condition (i). [1 mark.]
It's now easy to check that $f$ is one-to-one. Assume that $f(a)=f^{\prime}(b)$ for some $a, b \in \mathbb{P}$. Then, we have $f(b)=f(a)=f(a-b)+f(b)$ or $f(a-b)=0$. This implies that $a-b \in\{s \in$ $\mathbf{R} \mid f(s)=0\}=\{0\}$ or $a=b$, as desired. From (1) and the fact that $f$ is one-to-one, we deduce that $f(x)=x$ for all $x \in \mathbf{R}$. [1 mark.] This completes the proof.
|
{
"problem_match": "\n5. ",
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"solution_match": "# Solution 1."
}
| 88
| 842
|
2002
|
T1
|
5
| null |
APMO
|
Let R denote the set of all real numbers. Find all functions $f$ from R to R satisfying:
(i) there are only finitely many $s$ in R such that $f(s)=0$, and
(ii) $f\left(x^{4}+y\right)=x^{3} f(x)+f(f(y))$ for all $x, y$ in $\mathbf{R}$.
|
Again, the only such function is the identity function on R .
As in Solution 1, we first show that $f(f(y))=f(y), f(0)=0$, and $f\left(x^{4}\right)=x^{3} f(x)$. [2 marks.] From the latter follows
$$
f(x)=0 \Longrightarrow f\left(x^{4}\right)=0
$$
and from condition (i) we get that $f(x)=0$ only possibly for $x \in\{0,1,-1\}$. [1 mark.]
Next we prove
$$
f(a)=b \Longrightarrow f(\sqrt[4]{|a-b|})=0
$$
This is clear if $a=b$. If $a>b$ then
$$
\begin{aligned}
f(a) & =f((a-b)+b)=(a-b)^{3 / 4} f(\sqrt[4]{a-b})+f(f(b)) \\
& =(a-b)^{3 / 4} f(\sqrt[4]{a-b})+f(b) \\
& =(a-b)^{3 / 4} f(\sqrt[4]{a-b})+f(f(a)) \\
& =(a-b)^{3 / 4} f(\sqrt[4]{a-b})+f(a),
\end{aligned}
$$
so $(a-b)^{3 / 4} f(\sqrt[4]{a-b})=0$ which means $f(\sqrt[4]{|a-b|})=0$. If $a<b$ we get similarly
$$
\begin{aligned}
f(b) & =f((b-a)+a)=(b-a)^{3 / 4} f(\sqrt[4]{b-a})+f(f(a)) \\
& =(b-a)^{3 / 4} f(\sqrt[4]{b-a})+f(b)
\end{aligned}
$$
and again $f(\sqrt[4]{|a-b|})=0$. [2 marks.]
Thus $f(a)=b \Longrightarrow|a-b| \in\{0,1\}$. Suppose that $f(x)=x+b$ for some $x$, where $|b|=1$. Then from $f\left(x^{4}\right)=x^{3} f(x)$ and $f\left(x^{4}\right)=x^{4}+a$ for some $|a| \leq 1$ we get $x^{3}=a / b$, so $|x| \leq 1$. Thus $f(x)=x$ for all $x$ except possibly $x= \pm 1$. [ 1 mark.] But for example,
$$
f(1)=f\left(2^{4}-15\right)=2^{3} f(2)+f(f(-15))=2^{3} \cdot 2-15=1
$$
and
$$
f(-1)=f\left(2^{4}-17\right)=2^{3} f(2)+f(f(-17))=2^{3} \cdot 2-17=-1
$$
[1 mark.] This finishes the proof.
|
{
"problem_match": "\n5. ",
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"solution_match": "# Solution 2."
}
| 88
| 693
|
2003
|
T1
|
1
| null |
APMO
|
Let $a, b, c, d, e, f$ be real numbers such that the polynomial
$$
p(x)=x^{8}-4 x^{7}+7 x^{6}+a x^{5}+b x^{4}+c x^{3}+d x^{2}+e x+f
$$
factorises into eight linear factors $x-x_{i}$, with $x_{i}>0$ for $i=1,2, \ldots, 8$. Determine all possible values of $f$.
|
From
$$
x^{8}-4 x^{7}+7 x^{6}+a x^{5}+b x^{4}+c x^{3}+d x^{2}+e x+f=\left(x-x_{1}\right)\left(x-x_{2}\right) \ldots\left(x-x_{8}\right)
$$
we have
$$
\sum_{i=1}^{8} x_{i}=4 \quad \text { and } \quad \sum x_{i} x_{j}=7
$$
where the second sum is over all pairs $(i, j)$ of integers where $1 \leq i<j \leq 8$. Since this sum can also be written
$$
\frac{1}{2}\left[\left(\sum_{i=1}^{8} x_{i}\right)^{2}-\sum_{i=1}^{8} x_{i}^{2}\right]
$$
we get
$$
14=\left(\sum_{i=1}^{8} x_{i}\right)^{2}-\sum_{i=1}^{8} x_{i}^{2}=16-\sum_{i=1}^{8} x_{i}^{2}
$$
so
$$
\sum_{i=1}^{8} x_{i}^{2}=2 \quad \text { while } \quad \sum_{i=1}^{8} x_{i}=4 . \quad[3 \text { marks }]
$$
Now
$$
\sum_{i=1}^{8}\left(2 x_{i}-1\right)^{2}=4 \sum_{i=1}^{8} x_{i}^{2}-4 \sum_{i=1}^{8} x_{i}+8=4(2)-4(4)+8=0
$$
which forces $x_{i}=1 / 2$ for all $i$. [3 marks] Therefore
$$
f=\prod_{i=1}^{8} x_{i}=\left(\frac{1}{2}\right)^{8}=\frac{1}{256} . \quad[1 m x]
$$
Alternate solution: After obtaining (1) [3 marks], use Cauchy's inequality to get
$$
16=\left(x_{1} \cdot 1+x_{2} \cdot 1+\cdots+x_{8} \cdot 1\right)^{2} \leq\left(x_{1}^{2-}+x_{2}^{2}+\cdots+x_{8}^{2}\right)\left(1^{2}+1^{2}+\cdots+1^{2}\right)=8 \cdot 2=16
$$
or the power mean inequality to get
$$
\frac{1}{2}=\frac{1}{8} \sum_{i=1}^{8} x_{i} \leq\left(\frac{1}{8} \sum_{i=1}^{8} x_{i}^{2}\right)^{1 / 2}=\frac{1}{2} . \quad[2 \text { marks }]
$$
Either way, equality must hold, which can only happen if all the terms $x_{i}$ are equal, that is, if $x_{i}=1 / 2$ for all $i$. [1 mark] Thus $f=1 / 256$ as above. [ 1 mark]
|
{
"problem_match": "\n1. ",
"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl",
"solution_match": "# Solution."
}
| 117
| 769
|
2003
|
T1
|
2
| null |
APMO
|
Suppose $A B C D$ is a square piece of cardboard with side length $a$. On a plane are two parallel lines $\ell_{1}$ and $\ell_{2}$, which are also $a$ units apart. The square $A B C D$ is placed on the plane so that sides $A B$ and $A D$ intersect $\ell_{1}$ at $E$ and $F$ respectively. Also, sides $C B$ and $C D$ intersect $\ell_{2}$ at $G$ and $H$ respectively. Let the perimeters of $\triangle A E F$ and $\triangle C G H$ be $m_{1}$ and $m_{2}$ respectively. Prove that no matter how the square was placed, $m_{1}+m_{2}$ remains constant.
|
Without loss of generality, assume the square has side $a=1$. Let $\theta$ be the acute angle between $\ell_{1}$ (or $\ell_{2}$ ) and the sides $A B$ and $C D$ of the square. Then, letting $E F=x$ and $G H=y$, we have
$$
E A=x \cos \theta, \quad A F=x \sin \theta, \quad C H=y \cos \theta, \quad C G=y \sin \theta
$$
Thus
$$
m_{1}+m_{2}=(x+y)(\sin \theta+\cos \theta+1) . \quad[2 \text { marks }]
$$
Draw lines parallel to $\ell_{1}, \ell_{2}$ through $A$ and $C$ respectively. The distance between these lines is $\sin \theta+\cos \theta$ [1 mark], as can be seen by drawing a mutual perpendicular to these lines through $B$, say. Also, the altitudes from $A$ to $E F$ and from $C$ to $G H$ have lengths $x \sin \theta \cos \theta$ and $y \sin \theta \cos \theta$ respectively [ 1 mark]. Therefore the distance between $\ell_{1}$ and $\ell_{2}$ must be
$$
(\sin \theta+\cos \theta)-x \sin \theta \cos \theta-y \sin \theta \cos \theta
$$
But we are given that this distance is $a=1$, so
$$
(x+y) \sin \theta \cos \theta+1=\sin \theta+\cos \theta
$$
or
$$
x+y=\frac{\sin \theta+\cos \theta-1}{\sin \theta \cos \theta} \cdot \quad[1 \text { mark }]
$$
Therefore, by (1),
$$
\begin{aligned}
m_{1}+m_{2} & =\frac{(\sin \theta+\cos \theta-1)(\sin \theta+\cos \theta+1)}{\sin \theta \cos \theta} \\
& =\frac{\left(\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta\right)-1}{\sin \theta \cos \theta} \\
& =\frac{1+2 \sin \theta \cos \theta-1}{\sin \theta \cos \theta}=2 . \quad[2 \text { marks }]
\end{aligned}
$$
|
{
"problem_match": "\n2. ",
"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl",
"solution_match": "\nSolution 3."
}
| 173
| 552
|
2003
|
T1
|
3
| null |
APMO
|
Let $k \geq 14$ be an integer, and let $p_{k}$ be the largest prime number which is strictly less than $k$. You may assume that $p_{k} \geq 3 k / 4$. Let $n$ be a composite integer. Prove:
(a) if $n=2 p_{k}$, then $n$ does not divide $(n-k)$ !;
(b) if $n>2 p_{k}$, then $n$ divides $(n-k)$ !.
|
(a) Note that $n-k=2 p_{k}-k<2 p_{k}-p_{k}=p_{k}$, so $p_{k} \nmid(n-k)$ !, so $2 p_{k} \nless(n-k)$ !. [1 mark]
(b) Note that $n>2 p_{k} \geq 3 k / 2$ implies $k<2 n / 3$, so $n-k>n / 3$. So if we can find integers $a, b \geq 3$ such that $n=a b$ and $a \neq b$, then both $a$ and $b$ will appear separately in the product $(n-k)!=1 \times 2 \times \cdots \times(n-k)$, which means $n \mid(n-k)!$. Observe that $k \geq 14$ implies $p_{k} \geq 13$, so that $n>2 p_{k} \geq 26$.
If $n=2^{\alpha}$ for some integer $\alpha \geq 5$, then take $a=2^{2}, b=2^{\alpha-2}$. [ 1 mark] Otherwise, since $n \geq 26>16$, we can take $a$ to be an odd prime factor of $n$ and $b=n / a$ [1 mark], unless $b<3$ or $b=a$.
Case (i): $b<3$. Since $n$ is composite, this means $b=2$, so that $2 a=n>2 p_{k}$. As $a$ is a prime number and $p_{k}$ is the largest prime number which is strictly less than $k$, it follows that $a \geq k$. From $n-k=2 a-k \geq$ $2 a-a=a>2$ we see that $n=2 a$ divides into $(n-k)$. [ 2 marks]
Case (ii): $b=a$. Then $n=a^{2}$ and $a>6$ since $n \geq 26$. Thus $n-k>n / 3=a^{2} / 3>2 a$, so that both $a$ and $2 a$ appear among $\{1,2, \ldots, n-k\}$. Hence $n=a^{2}$ divides into $(n-k)!$. [2 marks]
|
{
"problem_match": "\n3. ",
"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl",
"solution_match": "\nSolution."
}
| 113
| 530
|
2003
|
T1
|
4
| null |
APMO
|
Let $a, b, c$ be the sides of a triangle, with $a+b+c=1$, and let $n \geq 2$ be an integer. Show that
$$
\sqrt[n]{a^{n}+b^{n}}+\sqrt[n]{b^{n}+c^{n}}+\sqrt[n]{c^{n}+a^{n}}<1+\frac{\sqrt[n]{2}}{2}
$$
|
Without loss of generality, assume $a \leq b \leq c$. As $a+b>c$, we have
$$
\frac{\sqrt[n]{2}}{2}=\frac{\sqrt[n]{2}}{2}(a+b+c)>\frac{\sqrt[n]{2}}{2}(c+c)=\sqrt[n]{2 c^{n}} \geq \sqrt[n]{b^{n}+c^{n}} \quad \quad[2 \text { marks }]
$$
As $a \leq c$ and $n \geq 2$, we have
$$
\begin{aligned}
\left(c^{n}+a^{n}\right)-\left(c+\frac{a}{2}\right)^{n} & =a^{n}-\sum_{k=1}^{n}\binom{n}{k} c^{n-k}\left(\frac{a}{2}\right)^{k} \\
& \leq\left[1-\sum_{k=1}^{n}\binom{n}{k}\left(\frac{1}{2}\right)^{k}\right] a^{n} \quad\left(\text { since } c^{n-k} \geq a^{n-k}\right) \\
& =\left[\left(1-\frac{n}{2}\right)-\sum_{k=2}^{n}\binom{n}{k}\left(\frac{1}{2}\right)^{k}\right] a^{n}<0
\end{aligned}
$$
Thus
$$
\sqrt[n]{c^{n}+a^{n}}<c+\frac{a}{2} . \quad[3 \text { marks }]
$$
Likewise
$$
\sqrt[n]{b^{n}+a^{n}}<b+\frac{a}{2} \quad \quad[1 \text { mark }]
$$
Adding (1), (2) and (3), we get
$$
\sqrt[n]{a^{n}+b^{n}}+\sqrt[n]{b^{n}+c^{n}}+\sqrt[n]{c^{n}+a^{n}}<\frac{\sqrt[n]{2}}{2}+c+\frac{a}{2}+b+\frac{a}{2}=1+\frac{\sqrt[n]{2}}{2} . \quad[1 \text { mark }]
$$
|
{
"problem_match": "\n4. ",
"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl",
"solution_match": "# Solution."
}
| 95
| 517
|
2003
|
T1
|
5
| null |
APMO
|
Given two positive integers $m$ and $n$, find the smallest positive integer $k$ such that among any $k$ people, either there are $2 m$ of them who form $m$ pairs of mutually acquainted people or there are $2 n$ of them forming $n$ pairs of mutually unacquainted people.
|
Let the smallest positive integer $k$ satisfying the condition of the problem be denoted $r(m, n)$. We shall show that
$$
r(m, n)=2(m+n)-\min \{m, n\}-1
$$
Observe that, by symmetry, $r(m, n)=r(n, m)$. Therefore it suffices to consider the case where $m \geq n$, and to prove that
$$
r(m, n)=2 m+n-1 . \quad[1 \text { mark }]
$$
First we prove that
$$
r(m, n) \geq 2 m+n-1
$$
by an example. Call a group of $k$ people, every two of whom are mutually acquainted, a $k$-clique. Consider a set of $2 m+n-2$ people consisting of a $(2 m-1)$-clique together with an additional $n-1$ people none of whom know anyone else. (Call such people isolated.) Then there are not $2 m$ people forming $m$ mutually acquainted pairs, and there also are not $2 n$ people forming $n$ mutually unacquainted pairs. Thus $r(m, n) \geq$ $(2 m-1)+(n-1)+1=2 m+n-1$ by the definition of $r(m, n)$. [1 mark]
To establish (1), we need to prove that $r(m, n) \leq 2 m+n-1$. To do this, we now show that
$$
r(m, n) \leq r(m-1, n-1)+3 \quad \text { for all } m \geq n \geq 2
$$
Let $G$ be a group of $t=r(m-1, n-1)+3$ people. Notice that
$$
t \geq 2(m-1)+(n-1)-1+3=2 m+n-1 \geq 2 m \geq 2 n
$$
If $G$ is a $t$-clique, then $G$ contains $2 m$ people forming $m$ mutually acquainted pairs, and if $G$ has only isolated people, then $G$ contains $2 n$ people forming $n$ mutually unacquainted pairs. Otherwise, there are three people in $G$, say $a, b$ and $c$, such that $a, b$ are acquainted but $a, c$ are not. Now consider the group $A$ obtained byremoving $a, b$ and $c$ from $G$. A has $t-3=r(m-1, n-1)$ people, so by the definition of $r(m-1, n-1)$, A either contains $2(m-1)$ people forming $m-1$ mutually acquainted pairs, or else contains $2(n-1)$ people forming $n-1$ mutually unacquainted pairs. In the former case, we add the acquainted pair $a, b$ to $A$ to form $m$ mutually acquainted pairs in $G$. In the latter case, we add the unacquainted pair $a, c$ to $A$ to form $n$ mutually unacquainted pairs in $G$. This proves (2). [3 marks]
Trivially, $r(s, 1)=2 s$ for all $s[\mathbf{1}$ mark], so $r(m, n) \leq 2 m+n-1$ holds whenever $n=1$. Proceeding by induction on $n$, by (2) we obtain
$$
r(m, n) \leq r(m-1, n-1)+3 \leq 2(m-1)+(n-1)-1+3=2 m+n-1
$$
which completes the proof. [1 mark]
Note. Give an additional 1 mark to any student who gets at most 5 marks by the above marking scheme, but in addition gives a valid argument that $r(2,2)=5$.
|
{
"problem_match": "\n5. ",
"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl",
"solution_match": "# Solution."
}
| 69
| 878
|
2004
|
T1
|
2
| null |
APMO
|
Let $O$ be the circumcentre and $H$ the orthocentre of an acute triangle $A B C$. Prove that the area of one of the triangles $\mathrm{AOH}, \mathrm{BOH}$ and COH is equal to the sum of the areas of the other two.
|
One can use barycentric coordinates: it is well known that
$$
\begin{gathered}
A=(1: 0: 0), \quad B=(0: 1: 0), \quad C=(0: 0: 1), \\
O=(\sin 2 A: \sin 2 B: \sin 2 C) \quad \text { and } \quad H=(\tan A: \tan B: \tan C) .
\end{gathered}
$$
Then the (signed) area of $A O H$ is proportional to
$$
\left|\begin{array}{ccc}
1 & 0 & 0 \\
\sin 2 A & \sin 2 B & \sin 2 C \\
\tan A & \tan B & \tan C
\end{array}\right|
$$
Adding all three expressions we find that the sum of the signed sums of the areas is a constant times
$$
\left|\begin{array}{ccc}
1 & 0 & 0 \\
\sin 2 A & \sin 2 B & \sin 2 C \\
\tan A & \tan B & \tan C
\end{array}\right|+\left|\begin{array}{ccc}
0 & 1 & 0 \\
\sin 2 A & \sin 2 B & \sin 2 C \\
\tan A & \tan B & \tan C
\end{array}\right|+\left|\begin{array}{ccc}
0 & 0 & 1 \\
\sin 2 A & \sin 2 B & \sin 2 C \\
\tan A & \tan B & \tan C
\end{array}\right|
$$
By multilinearity of the determinant, this sum equals
$$
\left|\begin{array}{ccc}
1 & 1 & 1 \\
\sin 2 A & \sin 2 B & \sin 2 C \\
\tan A & \tan B & \tan C
\end{array}\right|
$$
which contains, in its rows, the coordinates of the centroid, the circumcenter, and the orthocenter. Since these three points lie in the Euler line of $A B C$, the signed sum of the areas is 0 , which means that one of the areas of $A O H, B O H, C O H$ is the sum of the other two areas.
Comment: Both solutions can be adapted to prove a stronger result: if the centroid $G$ of triangle $A B C$ belongs to line $X Y$ then one of the areas of triangles $A X Y, B X Y$, and $C X Y$ is equal to the sum of the other two.
|
{
"problem_match": "# Problem 2",
"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl",
"solution_match": "# Solution 2"
}
| 63
| 583
|
2004
|
T1
|
3
| null |
APMO
|
Let a set $S$ of 2004 points in the plane be given, no three of which are collinear. Let $\mathcal{L}$ denote the set of all lines (extended indefinitely in both directions) determined by pairs of points from the set. Show that it is possible to colour the points of $S$ with at most two colours, such that for any points $p, q$ of $S$, the number of lines in $\mathcal{L}$ which separate $p$ from $q$ is odd if and only if $p$ and $q$ have the same colour.
Note: A line $\ell$ separates two points $p$ and $q$ if $p$ and $q$ lie on opposite sides of $\ell$ with neither point on $\ell$.
|
Choose any point $p$ from $S$ and color it, say, blue. Let $n(q, r)$ be the number of lines from $\mathcal{L}$ that separates $q$ and $r$. Then color any other point $q$ blue if $n(p, q)$ is odd and red if $n(p, q)$ is even.
Now it remains to show that $q$ and $r$ have the same color if and only if $n(q, r)$ is odd for all $q \neq p$ and $r \neq p$, which is equivalent to proving that $n(p, q)+n(p, r)+n(q, r)$ is always odd. For this purpose, consider the seven numbered regions defined by lines $p q$, $p r$, and $q r$ :
Any line that do not pass through any of points $p, q, r$ meets the sides $p q, q r, p r$ of triangle $p q r$ in an even number of points (two sides or no sides), so these lines do not affect the parity of $n(p, q)+n(p, r)+n(q, r)$. Hence the only lines that need to be considered are the ones that pass through one of vertices $p, q, r$ and cuts the opposite side in the triangle $p q r$.
Let $n_{i}$ be the number of points in region $i, p, q$, and $r$ excluded, as depicted in the diagram. Then the lines through $p$ that separate $q$ and $r$ are the lines passing through $p$ and points from regions 1,4 , and 7 . The same applies for $p, q$ and regions 2,5 , and 7 ; and $p, r$ and regions 3,6 , and 7. Therefore
$$
\begin{aligned}
n(p, q)+n(q, r)+n(p, r) & \equiv\left(n_{2}+n_{5}+n_{7}\right)+\left(n_{1}+n_{4}+n_{7}\right)+\left(n_{3}+n_{6}+n_{7}\right) \\
& \equiv n_{1}+n_{2}+n_{3}+n_{4}+n_{5}+n_{6}+n_{7}=2004-3 \equiv 1 \quad(\bmod 2)
\end{aligned}
$$
and the result follows.
Comment: The problem statement is also true if 2004 is replaced by any even number and is not true if 2004 is replaced by any odd number greater than 1.
|
{
"problem_match": "# Problem 3",
"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl",
"solution_match": "# Solution\n\n"
}
| 167
| 585
|
2004
|
T1
|
4
| null |
APMO
|
For a real number $x$, let $\lfloor x\rfloor$ stand for the largest integer that is less than or equal to $x$. Prove that
$$
\left\lfloor\frac{(n-1)!}{n(n+1)}\right\rfloor
$$
is even for every positive integer $n$.
|
Consider four cases:
- $n \leq 5$. Then $\left\lfloor\frac{(n-1)!}{n(n+1)}\right\rfloor=0$ is an even number.
- $n$ and $n+1$ are both composite (in particular, $n \geq 8$ ). Then $n=a b$ and $n+1=c d$ for $a, b, c, d \geq 2$. Moreover, since $n$ and $n+1$ are coprime, $a, b, c, d$ are all distinct and smaller than $n$, and one can choose $a, b, c, d$ such that exactly one of these four numbers is even. Hence $\frac{(n-1)!}{n(n+1)}$ is an integer. As $n \geq 8>6,(n-1)!$ has at least three even factors, so $\frac{(n-1)!}{n(n+1)}$ is an even integer.
- $n \geq 7$ is an odd prime. By Wilson's theorem, $(n-1)!\equiv-1(\bmod n)$, that is, $\frac{(n-1)!+1}{n}$ is an integer, as $\frac{(n-1)!+n+1}{n}=\frac{(n-1)!+1}{n}+1$ is. As before, $\frac{(n-1)!}{n+1}$ is an even integer; therefore $\frac{(n-1)!+n+1}{n+1}=\frac{(n-1)!}{n+1}+1$ is an odd integer.
Also, $n$ and $n+1$ are coprime and $n$ divides the odd integer $\frac{(n-1)!+n+1}{n+1}$, so $\frac{(n-1)!+n+1}{n(n+1)}$ is also an odd integer. Then
$$
\left\lfloor\frac{(n-1)!}{n(n+1)}\right\rfloor=\frac{(n-1)!+n+1}{n(n+1)}-1
$$
is even.
- $n+1 \geq 7$ is an odd prime. Again, since $n$ is composite, $\frac{(n-1)!}{n}$ is an even integer, and $\frac{(n-1)!+n}{n}$ is an odd integer. By Wilson's theorem, $n!\equiv-1(\bmod n+1) \Longleftrightarrow(n-1)!\equiv 1$ $(\bmod n+1)$. This means that $n+1$ divides $(n-1)!+n$, and since $n$ and $n+1$ are coprime, $n+1$ also divides $\frac{(n-1)!+n}{n}$. Then $\frac{(n-1)!+n}{n(n+1)}$ is also an odd integer and
$$
\left\lfloor\frac{(n-1)!}{n(n+1)}\right\rfloor=\frac{(n-1)!+n}{n(n+1)}-1
$$
is even.
|
{
"problem_match": "# Problem 4",
"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl",
"solution_match": "# Solution\n\n"
}
| 72
| 702
|
2004
|
T1
|
5
| null |
APMO
|
Prove that
$$
\left(a^{2}+2\right)\left(b^{2}+2\right)\left(c^{2}+2\right) \geq 9(a b+b c+c a)
$$
for all real numbers $a, b, c>0$.
|
Let $p=a+b+c, q=a b+b c+c a$, and $r=a b c$. The inequality simplifies to
$$
a^{2} b^{2} c^{2}+2\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2}\right)+4\left(a^{2}+b^{2}+c^{2}\right)+8-9(a b+b c+c a) \geq 0
$$
Since $a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2}=q^{2}-2 p r$ and $a^{2}+b^{2}+c^{2}=p^{2}-2 q$,
$$
r^{2}+2 q^{2}-4 p r+4 p^{2}-8 q+8-9 q \geq 0
$$
which simplifies to
$$
r^{2}+2 q^{2}+4 p^{2}-17 q-4 p r+8 \geq 0
$$
Bearing in mind that equality occurs for $a=b=c=1$, which means that, for instance, $p=3 r$, one can rewrite $(I)$ as
$$
\left(r-\frac{p}{3}\right)^{2}-\frac{10}{3} p r+\frac{35}{9} p^{2}+2 q^{2}-17 q+8 \geq 0
$$
Since $(a b-b c)^{2}+(b c-c a)^{2}+(c a-a b)^{2} \geq 0$ is equivalent to $q^{2} \geq 3 p r$, rewrite $(I I)$ as
$$
\left(r-\frac{p}{3}\right)^{2}+\frac{10}{9}\left(q^{2}-3 p r\right)+\frac{35}{9} p^{2}+\frac{8}{9} q^{2}-17 q+8 \geq 0
$$
Finally, $a=b=c=1$ implies $q=3$; then rewrite (III) as
$$
\left(r-\frac{p}{3}\right)^{2}+\frac{10}{9}\left(q^{2}-3 p r\right)+\frac{35}{9}\left(p^{2}-3 q\right)+\frac{8}{9}(q-3)^{2} \geq 0
$$
This final inequality is true because $q^{2} \geq 3 p r$ and $p^{2}-3 q=\frac{1}{2}\left[(a-b)^{2}+(b-c)^{2}+(c-a)^{2}\right] \geq 0$.
|
{
"problem_match": "# Problem 5",
"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl",
"solution_match": "# Solution 1"
}
| 64
| 633
|
2004
|
T1
|
5
| null |
APMO
|
Prove that
$$
\left(a^{2}+2\right)\left(b^{2}+2\right)\left(c^{2}+2\right) \geq 9(a b+b c+c a)
$$
for all real numbers $a, b, c>0$.
|
We prove the stronger inequality
$$
\left(a^{2}+2\right)\left(b^{2}+2\right)\left(c^{2}+2\right) \geq 3(a+b+c)^{2}
$$
which implies the proposed inequality because $(a+b+c)^{2} \geq 3(a b+b c+c a)$ is equivalent to $(a-b)^{2}+(b-c)^{2}+(c-a)^{2} \geq 0$, which is immediate.
The inequality $(*)$ is equivalent to
$$
\left(\left(b^{2}+2\right)\left(c^{2}+2\right)-3\right) a^{2}-6(b+c) a+2\left(b^{2}+2\right)\left(c^{2}+2\right)-3(b+c)^{2} \geq 0
$$
Seeing this inequality as a quadratic inequality in $a$ with positive leading coefficient $\left(b^{2}+2\right)\left(c^{2}+\right.$ 2) $-3=b^{2} c^{2}+2 b^{2}+2 c^{2}+1$, it suffices to prove that its discriminant is non-positive, which is equivalent to
$$
(3(b+c))^{2}-\left(\left(b^{2}+2\right)\left(c^{2}+2\right)-3\right)\left(2\left(b^{2}+2\right)\left(c^{2}+2\right)-3(b+c)^{2}\right) \leq 0
$$
This simplifies to
$$
-2\left(b^{2}+2\right)\left(c^{2}+2\right)+3(b+c)^{2}+6 \leq 0
$$
Now we look $(* *)$ as a quadratic inequality in $b$ with negative leading coefficient $-2 c^{2}-1$ :
$$
\left(-2 c^{2}-1\right) b^{2}+6 c b-c^{2}-2 \leq 0
$$
If suffices to show that the discriminant of $(* *)$ is non-positive, which is equivalent to
$$
9 c^{2}-\left(2 c^{2}+1\right)\left(c^{2}+2\right) \leq 0
$$
It simplifies to $-2\left(c^{2}-1\right)^{2} \leq 0$, which is true. The equality occurs for $c^{2}=1$, that is, $c=1$, for which $b=\frac{6 c}{2\left(2 c^{2}+1\right)}=1$, and $a=\frac{6(b+c)}{2\left(\left(b^{2}+2\right)\left(c^{2}+2\right)-3\right)}=1$.
|
{
"problem_match": "# Problem 5",
"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl",
"solution_match": "# Solution 2"
}
| 64
| 647
|
2004
|
T1
|
5
| null |
APMO
|
Prove that
$$
\left(a^{2}+2\right)\left(b^{2}+2\right)\left(c^{2}+2\right) \geq 9(a b+b c+c a)
$$
for all real numbers $a, b, c>0$.
|
Let $A, B, C$ angles in $(0, \pi / 2)$ such that $a=\sqrt{2} \tan A, b=\sqrt{2} \tan B$, and $c=\sqrt{2} \tan C$. Then the inequality is equivalent to
$$
4 \sec ^{2} A \sec ^{2} B \sec ^{2} C \geq 9(\tan A \tan B+\tan B \tan C+\tan C \tan A)
$$
Substituting $\sec x=\frac{1}{\cos x}$ for $x \in\{A, B, C\}$ and clearing denominators, the inequality is equivalent to
$$
\cos A \cos B \cos C(\sin A \sin B \cos C+\cos A \sin B \sin C+\sin A \cos B \sin C) \leq \frac{4}{9}
$$
Since
$$
\begin{aligned}
& \cos (A+B+C)=\cos A \cos (B+C)-\sin A \sin (B+C) \\
= & \cos A \cos B \cos C-\cos A \sin B \sin C-\sin A \cos B \sin C-\sin A \sin B \cos C,
\end{aligned}
$$
we rewrite our inequality as
$$
\cos A \cos B \cos C(\cos A \cos B \cos C-\cos (A+B+C)) \leq \frac{4}{9}
$$
The cosine function is concave down on $(0, \pi / 2)$. Therefore, if $\theta=\frac{A+B+C}{3}$, by the AM-GM inequality and Jensen's inequality,
$$
\cos A \cos B \cos C \leq\left(\frac{\cos A+\cos B+\cos C}{3}\right)^{3} \leq \cos ^{3} \frac{A+B+C}{3}=\cos ^{3} \theta
$$
Therefore, since $\cos A \cos B \cos C-\cos (A+B+C)=\sin A \sin B \cos C+\cos A \sin B \sin C+$ $\sin A \cos B \sin C>0$, and recalling that $\cos 3 \theta=4 \cos ^{3} \theta-3 \cos \theta$,
$\cos A \cos B \cos C(\cos A \cos B \cos C-\cos (A+B+C)) \leq \cos ^{3} \theta\left(\cos ^{3} \theta-\cos 3 \theta\right)=3 \cos ^{4} \theta\left(1-\cos ^{2} \theta\right)$. Finally, by AM-GM (notice that $1-\cos ^{2} \theta=\sin ^{2} \theta>0$ ),
$3 \cos ^{4} \theta\left(1-\cos ^{2} \theta\right)=\frac{3}{2} \cos ^{2} \theta \cdot \cos ^{2} \theta\left(2-2 \cos ^{2} \theta\right) \leq \frac{3}{2}\left(\frac{\cos ^{2} \theta+\cos ^{2} \theta+\left(2-2 \cos ^{2} \theta\right)}{3}\right)^{3}=\frac{4}{9}$,
and the result follows.
|
{
"problem_match": "# Problem 5",
"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl",
"solution_match": "# Solution 3"
}
| 64
| 759
|
2005
|
T1
|
2
| null |
APMO
|
Let $a, b$ and $c$ be positive real numbers such that $a b c=8$. Prove that
$$
\frac{a^{2}}{\sqrt{\left(1+a^{3}\right)\left(1+b^{3}\right)}}+\frac{b^{2}}{\sqrt{\left(1+b^{3}\right)\left(1+c^{3}\right)}}+\frac{c^{2}}{\sqrt{\left(1+c^{3}\right)\left(1+a^{3}\right)}} \geq \frac{4}{3} .
$$
|
Observe that
$$
\frac{1}{\sqrt{1+x^{3}}} \geq \frac{2}{2+x^{2}}
$$
In fact, this is equivalent to $\left(2+x^{2}\right)^{2} \geq 4\left(1+x^{3}\right)$, or $x^{2}(x-2)^{2} \geq 0$. Notice that equality holds in (1) if and only if $x=2$.
We substitute $x$ by $a, b, c$ in (1), respectively, to find
$$
\begin{gathered}
\frac{a^{2}}{\sqrt{\left(1+a^{3}\right)\left(1+b^{3}\right)}}+\frac{b^{2}}{\sqrt{\left(1+b^{3}\right)\left(1+c^{3}\right)}}+\frac{c^{2}}{\sqrt{\left(1+c^{3}\right)\left(1+a^{3}\right)}} \\
\geq \frac{4 a^{2}}{\left(2+a^{2}\right)\left(2+b^{2}\right)}+\frac{4 b^{2}}{\left(2+b^{2}\right)\left(2+c^{2}\right)}+\frac{4 c^{2}}{\left(2+c^{2}\right)\left(2+a^{2}\right)}
\end{gathered}
$$
We combine the terms on the right hand side of (2) to obtain
$$
\text { Left hand side of }(2) \geq \frac{2 S(a, b, c)}{36+S(a, b, c)}=\frac{2}{1+36 / S(a, b, c)}
$$
where $S(a, b, c):=2\left(a^{2}+b^{2}+c^{2}\right)+(a b)^{2}+(b c)^{2}+(c a)^{2}$. By AM-GM inequality, we have
$$
\begin{aligned}
a^{2}+b^{2}+c^{2} & \geq 3 \sqrt[3]{(a b c)^{2}}=12 \\
(a b)^{2}+(b c)^{2}+(c a)^{2} & \geq 3 \sqrt[3]{(a b c)^{4}}=48
\end{aligned}
$$
Note that the equalities holds if and only if $a=b=c=2$. The above inequalities yield
$$
S(a, b, c)=2\left(a^{2}+b^{2}+c^{2}\right)+(a b)^{2}+(b c)^{2}+(c a)^{2} \geq 72
$$
Therefore
$$
\frac{2}{1+36 / S(a, b, c)} \geq \frac{2}{1+36 / 72}=\frac{4}{3}
$$
which is the required inequality.
|
{
"problem_match": "\nProblem 2.",
"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl",
"solution_match": "(Solution)"
}
| 125
| 670
|
2005
|
T1
|
4
| null |
APMO
|
In a small town, there are $n \times n$ houses indexed by $(i, j)$ for $1 \leq i, j \leq n$ with $(1,1)$ being the house at the top left corner, where $i$ and $j$ are the row and column indices, respectively. At time 0 , a fire breaks out at the house indexed by $(1, c)$, where $c \leq \frac{n}{2}$. During each subsequent time interval $[t, t+1]$, the fire fighters defend a house which is not yet on fire while the fire spreads to all undefended neighbors of each house which was on fire at time $t$. Once a house is defended, it remains so all the time. The process ends when the fire can no longer spread. At most how many houses can be saved by the fire fighters? A house indexed by $(i, j)$ is a neighbor of a house indexed by $(k, \ell)$ if $|i-k|+|j-\ell|=1$.
|
At most $n^{2}+c^{2}-n c-c$ houses can be saved. This can be achieved under the following order of defending:
$$
\begin{gathered}
(2, c),(2, c+1) ;(3, c-1),(3, c+2) ;(4, c-2),(4, c+3) ; \ldots \\
(c+1,1),(c+1,2 c) ;(c+1,2 c+1), \ldots,(c+1, n)
\end{gathered}
$$
Under this strategy, there are
2 columns (column numbers $c, c+1$ ) at which $n-1$ houses are saved
2 columns (column numbers $c-1, c+2$ ) at which $n-2$ houses are saved
...
2 columns (column numbers $1,2 c$ ) at which $n-c$ houses are saved
$n-2 c$ columns (column numbers $n-2 c+1, \ldots, n$ ) at which $n-c$ houses are saved
Adding all these we obtain :
$$
2[(n-1)+(n-2)+\cdots+(n-c)]+(n-2 c)(n-c)=n^{2}+c^{2}-c n-c
$$
We say that a house indexed by $(i, j)$ is at level $t$ if $|i-1|+|j-c|=t$. Let $d(t)$ be the number of houses at level $t$ defended by time $t$, and $p(t)$ be the number of houses at levels greater than $t$ defended by time $t$. It is clear that
$$
p(t)+\sum_{i=1}^{t} d(i) \leq t \text { and } p(t+1)+d(t+1) \leq p(t)+1
$$
Let $s(t)$ be the number of houses at level $t$ which are not burning at time $t$. We prove that
$$
s(t) \leq t-p(t) \leq t
$$
for $1 \leq t \leq n-1$ by induction. It is obvious when $t=1$. Assume that it is true for $t=k$. The union of the neighbors of any $k-p(k)+1$ houses at level $k+1$ contains at least $k-p(k)+1$ vertices at level $k$. Since $s(k) \leq k-p(k)$, one of these houses at level $k$ is burning. Therefore, at most $k-p(k)$ houses at level $k+1$ have no neighbor burning. Hence we have
$$
\begin{aligned}
s(k+1) & \leq k-p(k)+d(k+1) \\
& =(k+1)-(p(k)+1-d(k+1)) \\
& \leq(k+1)-p(k+1)
\end{aligned}
$$
We now prove that the strategy given above is optimal. Since
$$
\sum_{t=1}^{n-1} s(t) \leq\binom{ n}{2}
$$
the maximum number of houses at levels less than or equal to $n-1$, that can be saved under any strategy is at most $\binom{n}{2}$, which is realized by the strategy above. Moreover, at levels bigger than $n-1$, every house is saved under the strategy above.
The following is an example when $n=11$ and $c=4$. The houses with $\bigcirc$ mark are burned. The houses with $\otimes$ mark are blocked ones and hence those and the houses below them are saved.
|
{
"problem_match": "\nProblem 4.",
"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl",
"solution_match": "(Solution)"
}
| 221
| 808
|
2005
|
T1
|
5
| null |
APMO
|
In a triangle $A B C$, points $M$ and $N$ are on sides $A B$ and $A C$, respectively, such that $M B=B C=C N$. Let $R$ and $r$ denote the circumradius and the inradius of the triangle $A B C$, respectively. Express the ratio $M N / B C$ in terms of $R$ and $r$.
|
Let $\omega, O$ and $I$ be the circumcircle, the circumcenter and the incenter of $A B C$, respectively. Let $D$ be the point of intersection of the line $B I$ and the circle $\omega$ such that $D \neq B$. Then $D$ is the midpoint of the arc $A C$. Hence $O D \perp C N$ and $O D=R$.
We first show that triangles $M N C$ and $I O D$ are similar. Because $B C=B M$, the line $B I$ (the bisector of $\angle M B C$ ) is perpendicular to the line $C M$. Because $O D \perp C N$ and $I D \perp M C$, it follows that
$$
\angle O D I=\angle N C M
$$
Let $\angle A B C=2 \beta$. In the triangle $B C M$, we have
$$
\frac{C M}{N C}=\frac{C M}{B C}=2 \sin \beta
$$
Since $\angle D I C=\angle D C I$, we have $I D=C D=A D$. Let $E$ be the point of intersection of the line $D O$ and the circle $\omega$ such that $E \neq D$. Then $D E$ is a diameter of $\omega$ and $\angle D E C=\angle D B C=\beta$. Thus we have
$$
\frac{D I}{O D}=\frac{C D}{O D}=\frac{2 R \sin \beta}{R}=2 \sin \beta .
$$
Combining equations (8), (9), and (10) shows that triangles $M N C$ and $I O D$ are similar. It follows that
$$
\frac{M N}{B C}=\frac{M N}{N C}=\frac{I O}{O D}=\frac{I O}{R} .
$$
The well-known Euler's formula states that
$$
O I^{2}=R^{2}-2 R r .
$$
Therefore,
$$
\frac{M N}{B C}=\sqrt{1-\frac{2 r}{R}}
$$
(Alternative Solution) Let $a$ (resp., $b, c$ ) be the length of $B C$ (resp., $A C, A B$ ). Let $\alpha$ (resp., $\beta, \gamma$ ) denote the angle $\angle B A C$ (resp., $\angle A B C, \angle A C B$ ). By introducing coordinates $B=(0,0), C=(a, 0)$, it is immediate that the coordinates of $M$ and $N$ are
$$
M=(a \cos \beta, a \sin \beta), \quad N=(a-a \cos \gamma, a \sin \gamma)
$$
respectively. Therefore,
$$
\begin{aligned}
(M N / B C)^{2} & =\left[(a-a \cos \gamma-a \cos \beta)^{2}+(a \sin \gamma-a \sin \beta)^{2}\right] / a^{2} \\
& =(1-\cos \gamma-\cos \beta)^{2}+(\sin \gamma-\sin \beta)^{2} \\
& =3-2 \cos \gamma-2 \cos \beta+2(\cos \gamma \cos \beta-\sin \gamma \sin \beta) \\
& =3-2 \cos \gamma-2 \cos \beta+2 \cos (\gamma+\beta) \\
& =3-2 \cos \gamma-2 \cos \beta-2 \cos \alpha \\
& =3-2(\cos \gamma+\cos \beta+\cos \alpha) .
\end{aligned}
$$
Now we claim
$$
\cos \gamma+\cos \beta+\cos \alpha=\frac{r}{R}+1
$$
From
$$
\begin{aligned}
& a=b \cos \gamma+c \cos \beta \\
& b=c \cos \alpha+a \cos \gamma \\
& c=a \cos \beta+b \cos \alpha
\end{aligned}
$$
we get
$$
a(1+\cos \alpha)+b(1+\cos \beta)+c(1+\cos \gamma)=(a+b+c)(\cos \alpha+\cos \beta+\cos \gamma)
$$
Thus
$$
\begin{aligned}
& \cos \alpha+\cos \beta+\cos \gamma \\
& =\frac{1}{a+b+c}(a(1+\cos \alpha)+b(1+\cos \beta)+c(1+\cos \gamma)) \\
& =\frac{1}{a+b+c}\left(a\left(1+\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)+b\left(1+\frac{a^{2}+c^{2}-b^{2}}{2 a c}\right)+c\left(1+\frac{a^{2}+b^{2}-c^{2}}{2 a b}\right)\right) \\
& =\frac{1}{a+b+c}\left(a+b+c+\frac{a^{2}\left(b^{2}+c^{2}-a^{2}\right)+b^{2}\left(a^{2}+c^{2}-b^{2}\right)+c^{2}\left(a^{2}+b^{2}-c^{2}\right)}{2 a b c}\right) \\
& =1+\frac{2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} a^{2}-a^{4}-b^{4}-c^{4}}{2 a b c(a+b+c)}
\end{aligned}
$$
On the other hand, from $R=\frac{a}{2 \sin \alpha}$ it follows that
$$
\begin{aligned}
R^{2} & =\frac{a^{2}}{4\left(1-\cos ^{2} \alpha\right)}=\frac{a^{2}}{4\left(1-\left(\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)^{2}\right)} \\
& =\frac{a^{2} b^{2} c^{2}}{2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} a^{2}-a^{4}-b^{4}-c^{4}}
\end{aligned}
$$
Also from $\frac{1}{2}(a+b+c) r=\frac{1}{2} b c \sin \alpha$, it follows that
$$
\begin{aligned}
r^{2} & =\frac{b^{2} c^{2}\left(1-\cos ^{2} \alpha\right)}{(a+b+c)^{2}}=\frac{b^{2} c^{2}\left(1-\left(\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)^{2}\right)}{(a+b+c)^{2}} \\
& =\frac{2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} a^{2}-a^{4}-b^{4}-c^{4}}{4(a+b+c)^{2}}
\end{aligned}
$$
Combining (19), (20) and (21), we get (16) as desired.
Finally, by (15) and (16) we have
$$
\frac{M N}{B C}=\sqrt{1-\frac{2 r}{R}}
$$
Another proof of (16) from R.A. Johnson's "Advanced Euclidean Geometry" ${ }^{1}$ :
Construct the perpendicular bisectors $O D, O E, O F$, where $D, E, F$ are the midpoints of $B C, C A, A B$, respectively. By Ptolemy's Theorem applied to the cyclic quadrilateral $O E A F$, we get
$$
\frac{a}{2} \cdot R=\frac{b}{2} \cdot O F+\frac{c}{2} \cdot O E
$$
Similarly
$$
\frac{b}{2} \cdot R=\frac{c}{2} \cdot O D+\frac{a}{2} \cdot O F, \quad \frac{c}{2} \cdot R=\frac{a}{2} \cdot O E+\frac{b}{2} \cdot O D .
$$
Adding, we get
$$
s R=O D \cdot \frac{b+c}{2}+O E \cdot \frac{c+a}{2}+O F \cdot \frac{a+b}{2}
$$
where $s$ is the semiperimeter. But also, the area of triangle $O B C$ is $O D \cdot \frac{a}{2}$, and adding similar formulas for the areas of triangles $O C A$ and $O A B$ gives
$$
r s=\triangle A B C=O D \cdot \frac{a}{2}+O E \cdot \frac{b}{2}+O F \cdot \frac{c}{2}
$$
Adding (23) and (24) gives $s(R+r)=s(O D+O E+O F)$, or
$$
O D+O E+O F=R+r .
$$
Since $O D=R \cos A$ etc., (16) follows.
[^0]
[^0]: ${ }^{1}$ This proof was introduced to the coordinating country by Professor Bill Sands of Canada.
|
{
"problem_match": "\nProblem 5.",
"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl",
"solution_match": "(Solution)"
}
| 86
| 2,138
|
2006
|
T1
|
2
| null |
APMO
|
Prove that every positive integer can be written as a finite sum of distinct integral powers of the golden mean $\tau=\frac{1+\sqrt{5}}{2}$. Here, an integral power of $\tau$ is of the form $\tau^{i}$, where $i$ is an integer (not necessarily positive).
|
We will prove this statement by induction using the equality
$$
\tau^{2}=\tau+1
$$
If $n=1$, then $1=\tau^{0}$. Suppose that $n-1$ can be written as a finite sum of integral powers of $\tau$, say
$$
n-1=\sum_{i=-k}^{k} a_{i} \tau^{i}
$$
where $a_{i} \in\{0,1\}$ and $n \geq 2$. We will write (1) as
$$
n-1=a_{k} \cdots a_{1} a_{0} \cdot a_{-1} a_{-2} \cdots a_{-k}
$$
For example,
$$
1=1.0=0.11=0.1011=0.101011
$$
Firstly, we will prove that we may assume that in (2) we have $a_{i} a_{i+1}=0$ for all $i$ with $-k \leq i \leq k-1$. Indeed, if we have several occurrences of 11 , then we take the leftmost such occurrence. Since we may assume that it is preceded by a 0 , we can replace 011 with 100 using the identity $\tau^{i+1}+\tau^{i}=\tau^{i+2}$. By doing so repeatedly, if necessary, we will eliminate all occurrences of two 1's standing together. Now we have the representation
$$
n-1=\sum_{i=-K}^{K} b_{i} \tau^{i}
$$
where $b_{i} \in\{0,1\}$ and $b_{i} b_{i+1}=0$.
If $b_{0}=0$ in (3), then we just add $1=\tau^{0}$ to both sides of (3) and we are done.
Suppose now that there is 1 in the unit position of (3), that is $b_{0}=1$. If there are two 0 's to the right of it, i.e.
$$
n-1=\cdots 1.00 \cdots
$$
then we can replace 1.00 with 0.11 because $1=\tau^{-1}+\tau^{-2}$, and we are done because we obtain 0 in the unit position. Thus we may assume that
$$
n-1=\cdots 1.010 \cdots
$$
Again, if we have $n-1=\cdots 1.0100 \cdots$, we may rewrite it as
$$
n-1=\cdots 1.0100 \cdots=\cdots 1.0011 \cdots=\cdots 0.1111 \cdots
$$
and obtain 0 in the unit position. Therefore, we may assume that
$$
n-1=\cdots 1.01010 \cdots
$$
Since the number of 1's is finite, eventually we will obtain an occurrence of 100 at the end, i.e.
$$
n-1=\cdots 1.01010 \cdots 100
$$
Then we can shift all 1's to the right to obtain 0 in the unit position, i.e.
$$
n-1=\cdots 0.11 \cdots 11
$$
and we are done.
|
{
"problem_match": "\nProblem 2.",
"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl",
"solution_match": "(Solution)"
}
| 67
| 782
|
2006
|
T1
|
3
| null |
APMO
|
Let $p \geq 5$ be a prime and let $r$ be the number of ways of placing $p$ checkers on a $p \times p$ checkerboard so that not all checkers are in the same row (but they may all be in the same column). Show that $r$ is divisible by $p^{5}$. Here, we assume that all the checkers are identical.
|
Note that $r=\binom{p^{2}}{p}-p$. Hence, it suffices to show that
$$
\left(p^{2}-1\right)\left(p^{2}-2\right) \cdots\left(p^{2}-(p-1)\right)-(p-1)!\equiv 0 \quad\left(\bmod p^{4}\right)
$$
Now, let
$$
f(x):=(x-1)(x-2) \cdots(x-(p-1))=x^{p-1}+s_{p-2} x^{p-2}+\cdots+s_{1} x+s_{0} .
$$
Then the congruence equation (1) is same as $f\left(p^{2}\right)-s_{0} \equiv 0\left(\bmod p^{4}\right)$. Therefore, it suffices to show that $s_{1} p^{2} \equiv 0\left(\bmod p^{4}\right)$ or $s_{1} \equiv 0\left(\bmod p^{2}\right)$.
Since $a^{p-1} \equiv 1(\bmod p)$ for all $1 \leq a \leq p-1$, we can factor
$$
x^{p-1}-1 \equiv(x-1)(x-2) \cdots(x-(p-1)) \quad(\bmod p)
$$
Comparing the coefficients of the left hand side of (3) with those of the right hand side of (2), we obtain $p \mid s_{i}$ for all $1 \leq i \leq p-2$ and $s_{0} \equiv-1(\bmod p)$. On the other hand, plugging $p$ for $x$ in (2), we get
$$
f(p)=(p-1)!=s_{0}=p^{p-1}+s_{p-2} p^{p-2}+\cdots+s_{1} p+s_{0}
$$
which implies
$$
p^{p-1}+s_{p-2} p^{p-2}+\cdots+s_{2} p^{2}=-s_{1} p
$$
Since $p \geq 5, p \mid s_{2}$ and hence $s_{1} \equiv 0\left(\bmod p^{2}\right)$ as desired.
|
{
"problem_match": "\nProblem 3.",
"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl",
"solution_match": "(Solution)"
}
| 87
| 534
|
2006
|
T1
|
4
| null |
APMO
|
Let $A, B$ be two distinct points on a given circle $O$ and let $P$ be the midpoint of the line segment $A B$. Let $O_{1}$ be the circle tangent to the line $A B$ at $P$ and tangent to the circle $O$. Let $\ell$ be the tangent line, different from the line $A B$, to $O_{1}$ passing through $A$. Let $C$ be the intersection point, different from $A$, of $\ell$ and $O$. Let $Q$ be the midpoint of the line segment $B C$ and $O_{2}$ be the circle tangent to the line $B C$ at $Q$ and tangent to the line segment $A C$. Prove that the circle $O_{2}$ is tangent to the circle $O$.
|
Let $S$ be the tangent point of the circles $O$ and $O_{1}$ and let $T$ be the intersection point, different from $S$, of the circle $O$ and the line $S P$. Let $X$ be the tangent point of $\ell$ to $O_{1}$ and let $M$ be the midpoint of the line segment $X P$. Since $\angle T B P=\angle A S P$, the triangle $T B P$ is similar to the triangle $A S P$. Therefore,
$$
\frac{P T}{P B}=\frac{P A}{P S}
$$
Since the line $\ell$ is tangent to the circle $O_{1}$ at $X$, we have
$$
\angle S P X=90^{\circ}-\angle X S P=90^{\circ}-\angle A P M=\angle P A M
$$
which implies that the triangle $P A M$ is similar to the triangle $S P X$. Consequently,
$$
\frac{X S}{X P}=\frac{M P}{M A}=\frac{X P}{2 M A} \quad \text { and } \quad \frac{X P}{P S}=\frac{M A}{A P}
$$
From this and the above observation follows
$$
\frac{X S}{X P} \cdot \frac{P T}{P B}=\frac{X P}{2 M A} \cdot \frac{P A}{P S}=\frac{X P}{2 M A} \cdot \frac{M A}{X P}=\frac{1}{2} .
$$
Let $A^{\prime}$ be the intersection point of the circle $O$ and the perpendicular bisector of the chord $B C$ such that $A, A^{\prime}$ are on the same side of the line $B C$, and $N$ be the intersection point of the lines $A^{\prime} Q$ and $C T$. Since
$$
\angle N C Q=\angle T C B=\angle T C A=\angle T B A=\angle T B P
$$
and
$$
\angle C A^{\prime} Q=\frac{\angle C A B}{2}=\frac{\angle X A P}{2}=\angle P A M=\angle S P X,
$$
the triangle $N C Q$ is similar to the triangle $T B P$ and the triangle $C A^{\prime} Q$ is similar to the triangle $S P X$. Therefore
$$
\frac{Q N}{Q C}=\frac{P T}{P B} \quad \text { and } \quad \frac{Q C}{Q A^{\prime}}=\frac{X S}{X P} .
$$
and hence $Q A^{\prime}=2 Q N$ by (1). This implies that $N$ is the midpoint of the line segment $Q A^{\prime}$. Let the circle $O_{2}$ touch the line segment $A C$ at $Y$. Since
$$
\angle A C N=\angle A C T=\angle B C T=\angle Q C N
$$
and $|C Y|=|C Q|$, the triangles $Y C N$ and $Q C N$ are congruent and hence $N Y \perp A C$ and $N Y=N Q=N A^{\prime}$. Therefore, $N$ is the center of the circle $O_{2}$, which completes the proof.
Remark: Analytic solutions are possible: For example, one can prove for a triangle $A B C$ inscribed in a circle $O$ that $A B=k(2+2 t), A C=k(1+2 t), B C=k(1+4 t)$ for some positive numbers $k, t$ if and only if there exists a circle $O_{1}$ such that $O_{1}$ is tangent to the side $A B$ at its midpoint, the side $A C$ and the circle $O$.
One obtains $A B=k^{\prime}\left(1+4 t^{\prime}\right), A C=k^{\prime}\left(1+2 t^{\prime}\right), B C=k^{\prime}\left(2+2 t^{\prime}\right)$ by substituting $t=1 / 4 t^{\prime}$ and $k=2 k^{\prime} t^{\prime}$. So, there exists a circle $O_{2}$ such that $O_{2}$ is tangent to the side $B C$ at its midpoint, the side $A C$ and the circle $O$.
In the above, $t=\tan ^{2} \alpha$ and $k=\frac{4 R \tan \alpha}{\left(1+\tan ^{2} \alpha\right)\left(1+4 \tan ^{2} \alpha\right)}$, where $R$ is the radius of $O$ and $\angle A=2 \alpha$. Furthermore, $t^{\prime}=\tan ^{2} \gamma$ and $k^{\prime}=\frac{4 R \tan \gamma}{\left(1+\tan ^{2} \gamma\right)\left(1+4 \tan ^{2} \gamma\right)}$, where $\angle C=2 \gamma$. Observe that $\sqrt{t t^{\prime}}=\tan \alpha \cdot \tan \gamma=\frac{X S}{X P} \cdot \frac{P T}{P B}=\frac{1}{2}$, which implies $t t^{\prime}=\frac{1}{4}$. It is now routine easy to check that $k=2 k^{\prime} t^{\prime}$.
|
{
"problem_match": "\nProblem 4.",
"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl",
"solution_match": "(Solution)"
}
| 176
| 1,259
|
2006
|
T1
|
5
| null |
APMO
|
In a circus, there are $n$ clowns who dress and paint themselves up using a selection of 12 distinct colours. Each clown is required to use at least five different colours. One day, the ringmaster of the circus orders that no two clowns have exactly the same set
of colours and no more than 20 clowns may use any one particular colour. Find the largest number $n$ of clowns so as to make the ringmaster's order possible.
|
Let $C$ be the set of $n$ clowns. Label the colours $1,2,3, \ldots, 12$. For each $i=1,2, \ldots, 12$, let $E_{i}$ denote the set of clowns who use colour $i$. For each subset $S$ of $\{1,2, \ldots, 12\}$, let $E_{S}$ be the set of clowns who use exactly those colours in $S$. Since $S \neq S^{\prime}$ implies $E_{S} \cap E_{S^{\prime}}=\emptyset$, we have
$$
\sum_{S}\left|E_{S}\right|=|C|=n
$$
where $S$ runs over all subsets of $\{1,2, \ldots, 12\}$. Now for each $i$,
$$
E_{S} \subseteq E_{i} \quad \text { if and only if } \quad i \in S
$$
and hence
$$
\left|E_{i}\right|=\sum_{i \in S}\left|E_{S}\right|
$$
By assumption, we know that $\left|E_{i}\right| \leq 20$ and that if $E_{S} \neq \emptyset$, then $|S| \geq 5$. From this we obtain
$$
20 \times 12 \geq \sum_{i=1}^{12}\left|E_{i}\right|=\sum_{i=1}^{12}\left(\sum_{i \in S}\left|E_{S}\right|\right) \geq 5 \sum_{S}\left|E_{S}\right|=5 n
$$
Therefore $n \leq 48$.
Now, define a sequence $\left\{c_{i}\right\}_{i=1}^{52}$ of colours in the following way:
$1234|5678| 9101112 \mid$
$4123|8567| 1291011 \mid$
$3412|7856| 1112910 \mid$
$2341|6785| 1011129 \mid 1234$
The first row lists $c_{1}, \ldots, c_{12}$ in order, the second row lists $c_{13}, \ldots, c_{24}$ in order, the third row lists $c_{25}, \ldots, c_{36}$ in order, and finally the last row lists $c_{37}, \ldots, c_{52}$ in order. For each $j, 1 \leq j \leq 48$, assign colours $c_{j}, c_{j+1}, c_{j+2}, c_{j+3}, c_{j+4}$ to the $j$-th clown. It is easy to check that this assignment satisfies all conditions given above. So, 48 is the largest for $n$.
Remark: The fact that $n \leq 48$ can be obtained in a much simpler observation that
$$
5 n \leq 12 \times 20=240
$$
There are many other ways of constructing 48 distinct sets consisting of 5 colours. For example, consider the sets
$$
\begin{array}{cccc}
\{1,2,3,4,5,6\}, & \{3,4,5,6,7,8\}, & \{5,6,7,8,9,10\}, & \{7,8,9,10,11,12\}, \\
\{9,10,11,12,1,2\}, & \{11,12,1,2,3,4\}, & \{1,2,5,6,9,10\}, & \{3,4,7,8,11,12\} .
\end{array}
$$
Each of the above 8 sets has 6 distinct subsets consisting of exactly 5 colours. It is easy to check that the 48 subsets obtained in this manner are all distinct.
|
{
"problem_match": "\nProblem 5.",
"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl",
"solution_match": "(Solution)"
}
| 99
| 972
|
2007
|
T1
|
3
| null |
APMO
|
Consider $n$ disks $C_{1}, C_{2}, \ldots, C_{n}$ in a plane such that for each $1 \leq i<n$, the center of $C_{i}$ is on the circumference of $C_{i+1}$, and the center of $C_{n}$ is on the circumference of $C_{1}$. Define the score of such an arrangement of $n$ disks to be the number of pairs $(i, j)$ for which $C_{i}$ properly contains $C_{j}$. Determine the maximum possible score.
|
The answer is $(n-1)(n-2) / 2$.
Let's call a set of $n$ disks satisfying the given conditions an $n$-configuration. For an $n$ configuration $\mathcal{C}=\left\{C_{1}, \ldots, C_{n}\right\}$, let $S_{\mathcal{C}}=\left\{(i, j) \mid C_{i}\right.$ properly contains $\left.C_{j}\right\}$. So, the score of an $n$-configuration $\mathcal{C}$ is $\left|S_{\mathcal{C}}\right|$.
We'll show that (i) there is an $n$-configuration $\mathcal{C}$ for which $\left|S_{\mathcal{C}}\right|=(n-1)(n-2) / 2$, and that (ii) $\left|S_{\mathcal{C}}\right| \leq(n-1)(n-2) / 2$ for any $n$-configuration $\mathcal{C}$.
Let $C_{1}$ be any disk. Then for $i=2, \ldots, n-1$, take $C_{i}$ inside $C_{i-1}$ so that the circumference of $C_{i}$ contains the center of $C_{i-1}$. Finally, let $C_{n}$ be a disk whose center is on the circumference of $C_{1}$ and whose circumference contains the center of $C_{n-1}$. This gives $S_{\mathcal{C}}=\{(i, j) \mid 1 \leq i<j \leq n-1\}$ of size $(n-1)(n-2) / 2$, which proves (i).
For any $n$-configuration $\mathcal{C}, S_{\mathcal{C}}$ must satisfy the following properties:
(1) $(i, i) \notin S_{\mathcal{C}}$,
(2) $(i+1, i) \notin S_{\mathcal{C}},(1, n) \notin S_{\mathcal{C}}$,
(3) if $(i, j),(j, k) \in S_{\mathcal{C}}$, then $(i, k) \in S_{\mathcal{C}}$,
(4) if $(i, j) \in S_{\mathcal{C}}$, then $(j, i) \notin S_{\mathcal{C}}$.
Now we show that a set $G$ of ordered pairs of integers between 1 and $n$, satisfying the conditions $(1) \sim(4)$, can have no more than $(n-1)(n-2) / 2$ elements. Suppose that there exists a set $G$ that satisfies the conditions (1) $\sim(4)$, and has more than $(n-1)(n-2) / 2$ elements. Let $n$ be the least positive integer with which there exists such a set $G$. Note that $G$ must have $(i, i+1)$ for some $1 \leq i \leq n$ or $(n, 1)$, since otherwise $G$ can have at most
$$
\binom{n}{2}-n=\frac{n(n-3)}{2}<\frac{(n-1)(n-2)}{2}
$$
elements. Without loss of generality we may assume that $(n, 1) \in G$. Then $(1, n-1) \notin G$, since otherwise the condition (3) yields $(n, n-1) \in G$ contradicting the condition (2). Now let $G^{\prime}=\{(i, j) \in G \mid 1 \leq i, j \leq n-1\}$, then $G^{\prime}$ satisfies the conditions (1) (4), with $n-1$.
We now claim that $\left|G-G^{\prime}\right| \leq n-2$ :
Suppose that $\left|G-G^{\prime}\right|>n-2$, then $\left|G-G^{\prime}\right|=n-1$ and hence for each $1 \leq i \leq n-1$, either $(i, n)$ or $(n, i)$ must be in $G$. We already know that $(n, 1) \in G$ and $(n-1, n) \in G$ (because $(n, n-1) \notin G$ ) and this implies that $(n, n-2) \notin G$ and $(n-2, n) \in G$. If we keep doing this process, we obtain $(1, n) \in G$, which is a contradiction.
Since $\left|G-G^{\prime}\right| \leq n-2$, we obtain
$$
\left|G^{\prime}\right| \geq \frac{(n-1)(n-2)}{2}-(n-2)=\frac{(n-2)(n-3)}{2}
$$
This, however, contradicts the minimality of $n$, and hence proves (ii).
|
{
"problem_match": "\nProblem 3.",
"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl",
"solution_match": "\nSolution."
}
| 122
| 1,143
|
2007
|
T1
|
4
| null |
APMO
|
Let $x, y$ and $z$ be positive real numbers such that $\sqrt{x}+\sqrt{y}+\sqrt{z}=1$. Prove that
$$
\frac{x^{2}+y z}{\sqrt{2 x^{2}(y+z)}}+\frac{y^{2}+z x}{\sqrt{2 y^{2}(z+x)}}+\frac{z^{2}+x y}{\sqrt{2 z^{2}(x+y)}} \geq 1
$$
|
We first note that
$$
\begin{aligned}
\frac{x^{2}+y z}{\sqrt{2 x^{2}(y+z)}} & =\frac{x^{2}-x(y+z)+y z}{\sqrt{2 x^{2}(y+z)}}+\frac{x(y+z)}{\sqrt{2 x^{2}(y+z)}} \\
& =\frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}}+\sqrt{\frac{y+z}{2}} \\
& \geq \frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}}+\frac{\sqrt{y}+\sqrt{z}}{2} .
\end{aligned}
$$
Similarly, we have
$$
\begin{aligned}
& \frac{y^{2}+z x}{\sqrt{2 y^{2}(z+x)}} \geq \frac{(y-z)(y-x)}{\sqrt{2 y^{2}(z+x)}}+\frac{\sqrt{z}+\sqrt{x}}{2}, \\
& \frac{z^{2}+x y}{\sqrt{2 z^{2}(x+y)}} \geq \frac{(z-x)(z-y)}{\sqrt{2 z^{2}(x+y)}}+\frac{\sqrt{x}+\sqrt{y}}{2} .
\end{aligned}
$$
We now add (1) (3) to get
$$
\begin{aligned}
& \frac{x^{2}+y z}{\sqrt{2 x^{2}(y+z)}}+\frac{y^{2}+z x}{\sqrt{2 y^{2}(z+x)}}+\frac{z^{2}+x y}{\sqrt{2 z^{2}(x+y)}} \\
& \geq \frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}}+\frac{(y-z)(y-x)}{\sqrt{2 y^{2}(z+x)}}+\frac{(z-x)(z-y)}{\sqrt{2 z^{2}(x+y)}}+\sqrt{x}+\sqrt{y}+\sqrt{z} \\
& =\frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}}+\frac{(y-z)(y-x)}{\sqrt{2 y^{2}(z+x)}}+\frac{(z-x)(z-y)}{\sqrt{2 z^{2}(x+y)}}+1 .
\end{aligned}
$$
Thus, it suffices to show that
$$
\frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}}+\frac{(y-z)(y-x)}{\sqrt{2 y^{2}(z+x)}}+\frac{(z-x)(z-y)}{\sqrt{2 z^{2}(x+y)}} \geq 0 .
$$
Now, assume without loss of generality, that $x \geq y \geq z$. Then we have
$$
\frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}} \geq 0
$$
and
$$
\begin{aligned}
& \frac{(z-x)(z-y)}{\sqrt{2 z^{2}(x+y)}}+\frac{(y-z)(y-x)}{\sqrt{2 y^{2}(z+x)}}=\frac{(y-z)(x-z)}{\sqrt{2 z^{2}(x+y)}}-\frac{(y-z)(x-y)}{\sqrt{2 y^{2}(z+x)}} \\
& \geq \frac{(y-z)(x-y)}{\sqrt{2 z^{2}(x+y)}}-\frac{(y-z)(x-y)}{\sqrt{2 y^{2}(z+x)}}=(y-z)(x-y)\left(\frac{1}{\sqrt{2 z^{2}(x+y)}}-\frac{1}{\sqrt{2 y^{2}(z+x)}}\right)
\end{aligned}
$$
The last quantity is non-negative due to the fact that
$$
y^{2}(z+x)=y^{2} z+y^{2} x \geq y z^{2}+z^{2} x=z^{2}(x+y)
$$
This completes the proof.
|
{
"problem_match": "\nProblem 4.",
"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl",
"solution_match": "\nSolution."
}
| 110
| 913
|
2007
|
T1
|
4
| null |
APMO
|
Let $x, y$ and $z$ be positive real numbers such that $\sqrt{x}+\sqrt{y}+\sqrt{z}=1$. Prove that
$$
\frac{x^{2}+y z}{\sqrt{2 x^{2}(y+z)}}+\frac{y^{2}+z x}{\sqrt{2 y^{2}(z+x)}}+\frac{z^{2}+x y}{\sqrt{2 z^{2}(x+y)}} \geq 1
$$
|
By Cauchy-Schwarz inequality,
$$
\begin{aligned}
& \left(\frac{x^{2}}{\sqrt{2 x^{2}(y+z)}}+\frac{y^{2}}{\sqrt{2 y^{2}(z+x)}}+\frac{z^{2}}{\sqrt{2 z^{2}(x+y)}}\right) \\
& \quad \times(\sqrt{2(y+z)}+\sqrt{2(z+x)}+\sqrt{2(x+y)}) \geq(\sqrt{x}+\sqrt{y}+\sqrt{z})^{2}=1
\end{aligned}
$$
and
$$
\begin{aligned}
& \left(\frac{y z}{\sqrt{2 x^{2}(y+z)}}+\frac{z x}{\sqrt{2 y^{2}(z+x)}}+\frac{x y}{\sqrt{2 z^{2}(x+y)}}\right) \\
& \quad \times(\sqrt{2(y+z)}+\sqrt{2(z+x)}+\sqrt{2(x+y)}) \geq\left(\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}\right)^{2}
\end{aligned}
$$
We now combine (5) and (6) to find
$$
\begin{aligned}
& \left(\frac{x^{2}+y z}{\sqrt{2 x^{2}(y+z)}}+\frac{y^{2}+z x}{\sqrt{2 y^{2}(z+x)}}+\frac{z^{2}+x y}{\sqrt{2 z^{2}(x+y)}}\right) \\
& \quad \times(\sqrt{2(x+y)}+\sqrt{2(y+z)}+\sqrt{2(z+x)}) \\
& \geq 1+\left(\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}\right)^{2} \geq 2\left(\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}\right) .
\end{aligned}
$$
Thus, it suffices to show that
$$
2\left(\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}\right) \geq \sqrt{2(y+z)}+\sqrt{2(z+x)}+\sqrt{2(x+y)}
$$
Consider the following inequality using AM-GM inequality
$$
\left[\sqrt{\frac{y z}{x}}+\left(\frac{1}{2} \sqrt{\frac{z x}{y}}+\frac{1}{2} \sqrt{\frac{x y}{z}}\right)\right]^{2} \geq 4 \sqrt{\frac{y z}{x}}\left(\frac{1}{2} \sqrt{\frac{z x}{y}}+\frac{1}{2} \sqrt{\frac{x y}{z}}\right)=2(y+z)
$$
or equivalently
$$
\sqrt{\frac{y z}{x}}+\left(\frac{1}{2} \sqrt{\frac{z x}{y}}+\frac{1}{2} \sqrt{\frac{x y}{z}}\right) \geq \sqrt{2(y+z)} .
$$
Similarly, we have
$$
\begin{aligned}
& \sqrt{\frac{z x}{y}}+\left(\frac{1}{2} \sqrt{\frac{x y}{z}}+\frac{1}{2} \sqrt{\frac{y z}{x}}\right) \geq \sqrt{2(z+x)} \\
& \sqrt{\frac{x y}{z}}+\left(\frac{1}{2} \sqrt{\frac{y z}{x}}+\frac{1}{2} \sqrt{\frac{z x}{y}}\right) \geq \sqrt{2(x+y)}
\end{aligned}
$$
Adding the last three inequalities, we get
$$
2\left(\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}\right) \geq \sqrt{2(y+z)}+\sqrt{2(z+x)}+\sqrt{2(x+y)} .
$$
This completes the proof.
|
{
"problem_match": "\nProblem 4.",
"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl",
"solution_match": "\nSecond solution."
}
| 110
| 960
|
2007
|
T1
|
5
| null |
APMO
|
A regular $(5 \times 5)$-array of lights is defective, so that toggling the switch for one light causes each adjacent light in the same row and in the same column as well as the light itself to change state, from on to off, or from off to on. Initially all the lights are switched off. After a certain number of toggles, exactly one light is switched on. Find all the possible positions of this light.
|
We assign the following first labels to the 25 positions of the lights:
| 1 | 1 | 0 | 1 | 1 |
| :--- | :--- | :--- | :--- | :--- |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
For each on-off combination of lights in the array, define its first value to be the sum of the first labels of those positions at which the lights are switched on. It is easy to check that toggling any switch always leads to an on-off combination of lights whose first value has the same parity(the remainder when divided by 2) as that of the previous on-off combination.
The $90^{\circ}$ rotation of the first labels gives us another labels (let us call it the second labels) which also makes the parity of the second value(the sum of the second labels of those positions at which the lights are switched on) invariant under toggling.
| 1 | 0 | 1 | 0 | 1 |
| :--- | :--- | :--- | :--- | :--- |
| 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
Since the parity of the first and the second values of the initial status is 0 , after certain number of toggles the parity must remain unchanged with respect to the first labels and the second labels as well. Therefore, if exactly one light is on after some number of toggles, the label of that position must be 0 with respect to both labels. Hence according to the above pictures, the possible positions are the ones marked with $*_{i}$ 's in the following picture:
| | | | | |
| :--- | :--- | :--- | :--- | :--- |
| | $*_{2}$ | | $*_{1}$ | |
| | | $*_{0}$ | | |
| | $*_{3}$ | | $*_{4}$ | |
| | | | | |
Now we demonstrate that all five positions are possible:
Toggling the positions checked by t (the order of toggling is irrelevant) in the first picture makes the center $\left(*_{0}\right)$ the only position with light on and the second picture makes the position $*_{1}$ the only position with light on. The other $*_{i}$ 's can be obtained by rotating the second picture appropriately.
| | t | | t | |
| :---: | :---: | :---: | :---: | :---: |
| t | t | | t | t |
| | t | | | |
| | | t | t | t |
| | | | t | |
|
{
"problem_match": "\nProblem 5.",
"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl",
"solution_match": "\nSolution."
}
| 91
| 660
|
2008
|
T1
|
1
| null |
APMO
|
Let $A B C$ be a triangle with $\angle A<60^{\circ}$. Let $X$ and $Y$ be the points on the sides $A B$ and $A C$, respectively, such that $C A+A X=C B+B X$ and $B A+A Y=B C+C Y$. Let $P$ be the point in the plane such that the lines $P X$ and $P Y$ are perpendicular to $A B$ and $A C$, respectively. Prove that $\angle B P C<120^{\circ}$.
|
Let $I$ be the incenter of $\triangle A B C$, and let the feet of the perpendiculars from $I$ to $A B$ and to $A C$ be $D$ and $E$, respectively. (Without loss of generality, we may assume that $A C$ is the longest side. Then $X$ lies on the line segment $A D$. Although $P$ may or may not lie inside $\triangle A B C$, the proof below works for both cases. Note that $P$ is on the line perpendicular to $A B$ passing through $X$.) Let $O$ be the midpoint of $I P$, and let the feet of the perpendiculars from $O$ to $A B$ and to $A C$ be $M$ and $N$, respectively. Then $M$ and $N$ are the midpoints of $D X$ and $E Y$, respectively.
The conditions on the points $X$ and $Y$ yield the equations
$$
A X=\frac{A B+B C-C A}{2} \quad \text { and } \quad A Y=\frac{B C+C A-A B}{2} .
$$
From $A D=A E=\frac{C A+A B-B C}{2}$, we obtain
$$
B D=A B-A D=A B-\frac{C A+A B-B C}{2}=\frac{A B+B C-C A}{2}=A X .
$$
Since $M$ is the midpoint of $D X$, it follows that $M$ is the midpoint of $A B$. Similarly, $N$ is the midpoint of $A C$. Therefore, the perpendicular bisectors of $A B$ and $A C$ meet at $O$, that is, $O$ is the circumcenter of $\triangle A B C$. Since $\angle B A C<60^{\circ}, O$ lies on the same side of $B C$ as the point $A$ and
$$
\angle B O C=2 \angle B A C
$$
We can compute $\angle B I C$ as follows:
$$
\begin{aligned}
\angle B I C & =180^{\circ}-\angle I B C-\angle I C B=180^{\circ}-\frac{1}{2} \angle A B C-\frac{1}{2} \angle A C B \\
& =180^{\circ}-\frac{1}{2}(\angle A B C+\angle A C B)=180^{\circ}-\frac{1}{2}\left(180^{\circ}-\angle B A C\right)=90^{\circ}+\frac{1}{2} \angle B A C
\end{aligned}
$$
It follows from $\angle B A C<60^{\circ}$ that
$$
2 \angle B A C<90^{\circ}+\frac{1}{2} \angle B A C, \quad \text { i.e., } \quad \angle B O C<\angle B I C \text {. }
$$
From this it follows that $I$ lies inside the circumcircle of the isosceles triangle $B O C$ because $O$ and $I$ lie on the same side of $B C$. However, as $O$ is the midpoint of $I P, P$ must lie outside the circumcircle of triangle $B O C$ and on the same side of $B C$ as $O$. Therefore
$$
\angle B P C<\angle B O C=2 \angle B A C<120^{\circ} .
$$
Remark. If one assumes that $\angle A$ is smaller than the other two, then it is clear that the line $P X$ (or the line perpendicular to $A B$ at $X$ if $P=X$ ) runs through the excenter $I_{C}$ of the excircle tangent to the side $A B$. Since $2 \angle A C I_{C}=\angle A C B$ and $B C<A C$, we have $2 \angle P C B>\angle C$. Similarly, $2 \angle P B C>\angle B$. Therefore,
$$
\angle B P C=180^{\circ}-(\angle P B C+\angle P C B)<180^{\circ}-\left(\frac{\angle B+\angle C}{2}\right)=90+\frac{\angle A}{2}<120^{\circ}
$$
In this way, a special case of the problem can be easily proved.
|
{
"problem_match": "\nProblem 1.",
"resource_path": "APMO/segmented/en-apmo2008_sol.jsonl",
"solution_match": "(Solution)"
}
| 123
| 998
|
2008
|
T1
|
4
| null |
APMO
|
Consider the function $f: \mathbb{N}_{0} \rightarrow \mathbb{N}_{0}$, where $\mathbb{N}_{0}$ is the set of all non-negative integers, defined by the following conditions:
(i) $f(0)=0$,
(ii) $f(2 n)=2 f(n)$ and
(iii) $f(2 n+1)=n+2 f(n)$ for all $n \geq 0$.
(a) Determine the three sets $L:=\{n \mid f(n)<f(n+1)\}, E:=\{n \mid f(n)=f(n+1)\}$, and $G:=\{n \mid f(n)>f(n+1)\}$.
(b) For each $k \geq 0$, find a formula for $a_{k}:=\max \left\{f(n): 0 \leq n \leq 2^{k}\right\}$ in terms of $k$.
|
(a) Let
$$
L_{1}:=\{2 k: k>0\}, \quad E_{1}:=\{0\} \cup\{4 k+1: k \geq 0\}, \quad \text { and } G_{1}:=\{4 k+3: k \geq 0\} .
$$
We will show that $L_{1}=L, E_{1}=E$, and $G_{1}=G$. It suffices to verify that $L_{1} \subseteq E, E_{1} \subseteq E$, and $G_{1} \subseteq G$ because $L_{1}, E_{1}$, and $G_{1}$ are mutually disjoint and $L_{1} \cup E_{1} \cup G_{1}=\mathbb{N}_{0}$.
Firstly, if $k>0$, then $f(2 k)-f(2 k+1)=-k<0$ and therefore $L_{1} \subseteq L$.
Secondly, $f(0)=0$ and
$$
\begin{aligned}
& f(4 k+1)=2 k+2 f(2 k)=2 k+4 f(k) \\
& f(4 k+2)=2 f(2 k+1)=2(k+2 f(k))=2 k+4 f(k)
\end{aligned}
$$
for all $k \geq 0$. Thus, $E_{1} \subseteq E$.
Lastly, in order to prove $G_{1} \subset G$, we claim that $f(n+1)-f(n) \leq n$ for all $n$. (In fact, one can prove a stronger inequality : $f(n+1)-f(n) \leq n / 2$.) This is clearly true for even $n$ from the definition since for $n=2 t$,
$$
f(2 t+1)-f(2 t)=t \leq n
$$
If $n=2 t+1$ is odd, then (assuming inductively that the result holds for all nonnegative $m<n$ ), we have
$$
\begin{aligned}
f(n+1)-f(n) & =f(2 t+2)-f(2 t+1)=2 f(t+1)-t-2 f(t) \\
& =2(f(t+1)-f(t))-t \leq 2 t-t=t<n .
\end{aligned}
$$
For all $k \geq 0$,
$$
\begin{aligned}
& f(4 k+4)-f(4 k+3)=f(2(2 k+2))-f(2(2 k+1)+1) \\
& =4 f(k+1)-(2 k+1+2 f(2 k+1))=4 f(k+1)-(2 k+1+2 k+4 f(k)) \\
& =4(f(k+1)-f(k))-(4 k+1) \leq 4 k-(4 k+1)<0 .
\end{aligned}
$$
This proves $G_{1} \subseteq G$.
(b) Note that $a_{0}=a_{1}=f(1)=0$. Let $k \geq 2$ and let $N_{k}=\left\{0,1,2, \ldots, 2^{k}\right\}$. First we claim that the maximum $a_{k}$ occurs at the largest number in $G \cap N_{k}$, that is, $a_{k}=f\left(2^{k}-1\right)$. We use mathematical induction on $k$ to prove the claim. Note that $a_{2}=f(3)=f\left(2^{2}-1\right)$.
Now let $k \geq 3$. For every even number $2 t$ with $2^{k-1}+1<2 t \leq 2^{k}$,
$$
f(2 t)=2 f(t) \leq 2 a_{k-1}=2 f\left(2^{k-1}-1\right)
$$
by induction hypothesis. For every odd number $2 t+1$ with $2^{k-1}+1 \leq 2 t+1<2^{k}$,
$$
\begin{aligned}
f(2 t+1) & =t+2 f(t) \leq 2^{k-1}-1+2 f(t) \\
& \leq 2^{k-1}-1+2 a_{k-1}=2^{k-1}-1+2 f\left(2^{k-1}-1\right)
\end{aligned}
$$
again by induction hypothesis. Combining ( $\dagger$ ), ( $\ddagger$ ) and
$$
f\left(2^{k}-1\right)=f\left(2\left(2^{k-1}-1\right)+1\right)=2^{k-1}-1+2 f\left(2^{k-1}-1\right)
$$
we may conclude that $a_{k}=f\left(2^{k}-1\right)$ as desired.
Furthermore, we obtain
$$
a_{k}=2 a_{k-1}+2^{k-1}-1
$$
for all $k \geq 3$. Note that this recursive formula for $a_{k}$ also holds for $k \geq 0,1$ and 2 . Unwinding this recursive formula, we finally get
$$
\begin{aligned}
a_{k} & =2 a_{k-1}+2^{k-1}-1=2\left(2 a_{k-2}+2^{k-2}-1\right)+2^{k-1}-1 \\
& =2^{2} a_{k-2}+2 \cdot 2^{k-1}-2-1=2^{2}\left(2 a_{k-3}+2^{k-3}-1\right)+2 \cdot 2^{k-1}-2-1 \\
& =2^{3} a_{k-3}+3 \cdot 2^{k-1}-2^{2}-2-1 \\
& \vdots \\
& =2^{k} a_{0}+k 2^{k-1}-2^{k-1}-2^{k-2}-\ldots-2-1 \\
& =k 2^{k-1}-2^{k}+1 \quad \text { for all } k \geq 0 .
\end{aligned}
$$
|
{
"problem_match": "\nProblem 4.",
"resource_path": "APMO/segmented/en-apmo2008_sol.jsonl",
"solution_match": "(Solution)"
}
| 214
| 1,458
|
2009
|
T1
|
2
| null |
APMO
|
Let $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$ be real numbers satisfying the following equations:
$$
\frac{a_{1}}{k^{2}+1}+\frac{a_{2}}{k^{2}+2}+\frac{a_{3}}{k^{2}+3}+\frac{a_{4}}{k^{2}+4}+\frac{a_{5}}{k^{2}+5}=\frac{1}{k^{2}} \text { for } k=1,2,3,4,5
$$
Find the value of $\frac{a_{1}}{37}+\frac{a_{2}}{38}+\frac{a_{3}}{39}+\frac{a_{4}}{40}+\frac{a_{5}}{41}$. (Express the value in a single fraction.)
|
Let $R(x):=\frac{a_{1}}{x^{2}+1}+\frac{a_{2}}{x^{2}+2}+\frac{a_{3}}{x^{2}+3}+\frac{a_{4}}{x^{2}+4}+\frac{a_{5}}{x^{2}+5}$. Then $R( \pm 1)=1$, $R( \pm 2)=\frac{1}{4}, R( \pm 3)=\frac{1}{9}, R( \pm 4)=\frac{1}{16}, R( \pm 5)=\frac{1}{25}$ and $R(6)$ is the value to be found. Let's put $P(x):=\left(x^{2}+1\right)\left(x^{2}+2\right)\left(x^{2}+3\right)\left(x^{2}+4\right)\left(x^{2}+5\right)$ and $Q(x):=R(x) P(x)$. Then for $k= \pm 1, \pm 2, \pm 3, \pm 4, \pm 5$, we get $Q(k)=R(k) P(k)=\frac{P(k)}{k^{2}}$, that is, $P(k)-k^{2} Q(k)=0$. Since $P(x)-x^{2} Q(x)$ is a polynomial of degree 10 with roots $\pm 1, \pm 2, \pm 3, \pm 4, \pm 5$, we get
$$
P(x)-x^{2} Q(x)=A\left(x^{2}-1\right)\left(x^{2}-4\right)\left(x^{2}-9\right)\left(x^{2}-16\right)\left(x^{2}-25\right)
$$
Putting $x=0$, we get $A=\frac{P(0)}{(-1)(-4)(-9)(-16)(-25)}=-\frac{1}{120}$. Finally, dividing both sides of $(*)$ by $P(x)$ yields
$$
1-x^{2} R(x)=1-x^{2} \frac{Q(x)}{P(x)}=-\frac{1}{120} \cdot \frac{\left(x^{2}-1\right)\left(x^{2}-4\right)\left(x^{2}-9\right)\left(x^{2}-16\right)\left(x^{2}-25\right)}{\left(x^{2}+1\right)\left(x^{2}+2\right)\left(x^{2}+3\right)\left(x^{2}+4\right)\left(x^{2}+5\right)}
$$
and hence that
$$
1-36 R(6)=-\frac{35 \times 32 \times 27 \times 20 \times 11}{120 \times 37 \times 38 \times 39 \times 40 \times 41}=-\frac{3 \times 7 \times 11}{13 \times 19 \times 37 \times 41}=-\frac{231}{374699}
$$
which implies $R(6)=\frac{187465}{6744582}$.
Remark. We can get $a_{1}=\frac{1105}{72}, a_{2}=-\frac{2673}{40}, a_{3}=\frac{1862}{15}, a_{4}=-\frac{1885}{18}, a_{5}=\frac{1323}{40}$ by solving the given system of linear equations, which is extremely messy and takes a lot of time.
|
{
"problem_match": "\nProblem 2.",
"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl",
"solution_match": "(Solution)"
}
| 204
| 869
|
2009
|
T1
|
3
| null |
APMO
|
Let three circles $\Gamma_{1}, \Gamma_{2}, \Gamma_{3}$, which are non-overlapping and mutually external, be given in the plane. For each point $P$ in the plane, outside the three circles, construct six points $A_{1}, B_{1}, A_{2}, B_{2}, A_{3}, B_{3}$ as follows: For each $i=1,2,3, A_{i}, B_{i}$ are distinct points on the circle $\Gamma_{i}$ such that the lines $P A_{i}$ and $P B_{i}$ are both tangents to $\Gamma_{i}$. Call the point $P$ exceptional if, from the construction, three lines $A_{1} B_{1}, A_{2} B_{2}, A_{3} B_{3}$ are concurrent. Show that every exceptional point of the plane, if exists, lies on the same circle.
|
Let $O_{i}$ be the center and $r_{i}$ the radius of circle $\Gamma_{i}$ for each $i=1,2,3$. Let $P$ be an exceptional point, and let the three corresponding lines $A_{1} B_{1}, A_{2} B_{2}, A_{3} B_{3}$ concur at $Q$. Construct the circle with diameter $P Q$. Call the circle $\Gamma$, its center $O$ and its radius $r$. We now claim that all exceptional points lie on $\Gamma$.
Let $P O_{1}$ intersect $A_{1} B_{1}$ in $X_{1}$. As $P O_{1} \perp A_{1} B_{1}$, we see that $X_{1}$ lies on $\Gamma$. As $P A_{1}$ is a tangent to $\Gamma_{1}$, triangle $P A_{1} O_{1}$ is right-angled and similar to triangle $A_{1} X_{1} O_{1}$. It follows that
$$
\frac{O_{1} X_{1}}{O_{1} A_{1}}=\frac{O_{1} A_{1}}{O_{1} P}, \quad \text { i.e., } \quad O_{1} X_{1} \cdot O_{1} P=O_{1} A_{1}^{2}=r_{1}^{2}
$$
On the other hand, $O_{1} X_{1} \cdot O_{1} P$ is also the power of $O_{1}$ with respect to $\Gamma$, so that
$$
r_{1}^{2}=O_{1} X_{1} \cdot O_{1} P=\left(O_{1} O-r\right)\left(O_{1} O+r\right)=O_{1} O^{2}-r^{2}
$$
and hence
$$
r^{2}=O O_{1}^{2}-r_{1}^{2}=\left(O O_{1}-r_{1}\right)\left(O O_{1}+r_{1}\right)
$$
Thus, $r^{2}$ is the power of $O$ with respect to $\Gamma_{1}$. By the same token, $r^{2}$ is also the power of $O$ with respect to $\Gamma_{2}$ and $\Gamma_{3}$. Hence $O$ must be the radical center of the three given circles. Since $r$, as the square root of the power of $O$ with respect to the three given circles, does not depend on $P$, it follows that all exceptional points lie on $\Gamma$.
Remark. In the event of the radical point being at infinity (and hence the three radical axes being parallel), there are no exceptional points in the plane, which is consistent with the statement of the problem.
|
{
"problem_match": "\nProblem 3.",
"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl",
"solution_match": "(Solution)"
}
| 199
| 623
|
2009
|
T1
|
4
| null |
APMO
|
Prove that for any positive integer $k$, there exists an arithmetic sequence
$$
\frac{a_{1}}{b_{1}}, \quad \frac{a_{2}}{b_{2}}, \ldots, \quad \frac{a_{k}}{b_{k}}
$$
of rational numbers, where $a_{i}, b_{i}$ are relatively prime positive integers for each $i=1,2, \ldots, k$, such that the positive integers $a_{1}, b_{1}, a_{2}, b_{2}, \ldots, a_{k}, b_{k}$ are all distinct.
|
For $k=1$, there is nothing to prove. Henceforth assume $k \geq 2$.
Let $p_{1}, p_{2}, \ldots, p_{k}$ be $k$ distinct primes such that
$$
k<p_{k}<\cdots<p_{2}<p_{1}
$$
and let $N=p_{1} p_{2} \cdots p_{k}$. By Chinese Remainder Theorem, there exists a positive integer $x$ satisfying
$$
x \equiv-i \quad\left(\bmod p_{i}\right)
$$
for all $i=1,2, \ldots, k$ and $x>N^{2}$. Consider the following sequence:
$$
\frac{x+1}{N}, \frac{x+2}{N}, \quad, \ldots, \frac{x+k}{N}
$$
This sequence is obviously an arithmetic sequence of positive rational numbers of length $k$. For each $i=1,2, \ldots, k$, the numerator $x+i$ is divisible by $p_{i}$ but not by $p_{j}$ for $j \neq i$, for otherwise $p_{j}$ divides $|i-j|$, which is not possible because $p_{j}>k>|i-j|$. Let
$$
a_{i}:=\frac{x+i}{p_{i}}, \quad b_{i}:=\frac{N}{p_{i}} \quad \text { for all } i=1,2, \ldots, k
$$
Then
$$
\frac{x+i}{N}=\frac{a_{i}}{b_{i}}, \quad \operatorname{gcd}\left(a_{i}, b_{i}\right)=1 \quad \text { for all } i=1,2, \ldots, k
$$
and all $b_{i}$ 's are distinct from each other. Moreover, $x>N^{2}$ implies
$$
a_{i}=\frac{x+i}{p_{i}}>\frac{N^{2}}{p_{i}}>N>\frac{N}{p_{j}}=b_{j} \quad \text { for all } i, j=1,2, \ldots, k
$$
and hence all $a_{i}$ 's are distinct from $b_{i}$ 's. It only remains to show that all $a_{i}$ 's are distinct from each other. This follows from
$$
a_{j}=\frac{x+j}{p_{j}}>\frac{x+i}{p_{j}}>\frac{x+i}{p_{i}}=a_{i} \quad \text { for all } i<j
$$
by our choice of $p_{1}, p_{2}, \ldots, p_{k}$. Thus, the arithmetic sequence
$$
\frac{a_{1}}{b_{1}}, \quad \frac{a_{2}}{b_{2}}, \ldots, \quad \frac{a_{k}}{b_{k}}
$$
of positive rational numbers satisfies the conditions of the problem.
Remark. Here is a much easier solution :
For any positive integer $k \geq 2$, consider the sequence
$$
\frac{(k!)^{2}+1}{k!}, \frac{(k!)^{2}+2}{k!}, \ldots, \frac{(k!)^{2}+k}{k!}
$$
Note that $\operatorname{gcd}\left(k!,(k!)^{2}+i\right)=i$ for all $i=1,2, \ldots, k$. So, taking
$$
a_{i}:=\frac{(k!)^{2}+i}{i}, \quad b_{i}:=\frac{k!}{i} \quad \text { for all } i=1,2, \ldots, k
$$
we have $\operatorname{gcd}\left(a_{i}, b_{i}\right)=1$ and
$$
a_{i}=\frac{(k!)^{2}+i}{i}>a_{j}=\frac{(k!)^{2}+j}{j}>b_{i}=\frac{k!}{i}>b_{j}=\frac{k!}{j}
$$
for any $1 \leq i<j \leq k$. Therefore this sequence satisfies every condition given in the problem.
|
{
"problem_match": "\nProblem 4.",
"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl",
"solution_match": "(Solution)"
}
| 136
| 959
|
2009
|
T1
|
5
| null |
APMO
|
Larry and Rob are two robots travelling in one car from Argovia to Zillis. Both robots have control over the steering and steer according to the following algorithm: Larry makes a $90^{\circ}$ left turn after every $\ell$ kilometer driving from start; Rob makes a $90^{\circ}$ right turn after every $r$ kilometer driving from start, where $\ell$ and $r$ are relatively prime positive integers. In the event of both turns occurring simultaneously, the car will keep going without changing direction. Assume that the ground is flat and the car can move in any direction.
Let the car start from Argovia facing towards Zillis. For which choices of the pair $(\ell, r)$ is the car guaranteed to reach Zillis, regardless of how far it is from Argovia?
|
Let Zillis be $d$ kilometers away from Argovia, where $d$ is a positive real number. For simplicity, we will position Argovia at $(0,0)$ and Zillis at $(d, 0)$, so that the car starts out facing east. We will investigate how the car moves around in the period of travelling the first $\ell r$ kilometers, the second $\ell r$ kilometers, ..., and so on. We call each period of travelling $\ell r$ kilometers a section. It is clear that the car will have identical behavior in every section except the direction of the car at the beginning.
Case 1: $\underline{\ell-r \equiv 2(\bmod 4)}$. After the first section, the car has made $\ell-1$ right turns and $r-1$ left turns, which is a net of $2(\equiv \ell-r(\bmod 4))$ right turns. Let the displacement vector for the first section be $(x, y)$. Since the car has rotated $180^{\circ}$, the displacement vector for the second section will be $(-x,-y)$, which will take the car back to $(0,0)$ facing east again. We now have our original situation, and the car has certainly never travelled further than lr kilometers from Argovia. So, the car cannot reach Zillis if it is further apart from Argovia.
Case 2: $\ell-r \equiv 1(\bmod 4)$. After the first section, the car has made a net of 1 right turn. Let the displacement vector for the first section again be $(x, y)$. This time the car has rotated $90^{\circ}$ clockwise. We can see that the displacements for the second, third and fourth section will be $(y,-x),(-x,-y)$ and $(-y, x)$, respectively, so after four sections the car is back at $(0,0)$ facing east. Since the car has certainly never travelled further than $2 \ell r$ kilometers from Argovia, the car cannot reach Zillis if it is further apart from Argovia.
Case 3: $\quad \ell-r \equiv 3(\bmod 4)$. An argument similar to that in Case 2 (switching the roles of left and right) shows that the car cannot reach Zillis if it is further apart from Argovia.
Case 4: $\quad \ell \equiv r(\bmod 4)$. The car makes a net turn of $0^{\circ}$ after each section, so it must be facing east. We are going to show that, after traversing the first section, the car will be at $(1,0)$. It will be useful to interpret the Cartesian plane as the complex plane, i.e. writing $x+i y$ for $(x, y)$, where $i=\sqrt{-1}$. We will denote the $k$-th kilometer of movement by $m_{k-1}$,
which takes values from the set $\{1, i,-1,-i\}$, depending on the direction. We then just have to show that
$$
\sum_{k=0}^{\ell r-1} m_{k}=1
$$
which implies that the car will get to Zillis no matter how far it is apart from Argovia.
Case $4 \mathrm{a}: \underline{\ell \equiv r \equiv 1(\bmod 4)}$. First note that for $k=0,1, \ldots, \ell r-1$,
$$
m_{k}=i^{\lfloor k / \ell\rfloor}(-i)^{\lfloor k / r\rfloor}
$$
since $\lfloor k / \ell\rfloor$ and $\lfloor k / r\rfloor$ are the exact numbers of left and right turns before the $(k+1)$ st kilometer, respectively. Let $a_{k}(\equiv k(\bmod \ell))$ and $b_{k}(\equiv k(\bmod r))$ be the remainders of $k$ when divided by $\ell$ and $r$, respectively. Then, since
$$
a_{k}=k-\left\lfloor\frac{k}{\ell}\right\rfloor \ell \equiv k-\left\lfloor\frac{k}{\ell}\right\rfloor \quad(\bmod 4) \quad \text { and } \quad b_{k}=k-\left\lfloor\frac{k}{r}\right\rfloor r \equiv k-\left\lfloor\frac{k}{r}\right\rfloor \quad(\bmod 4),
$$
we have $\lfloor k / \ell\rfloor \equiv k-a_{k}(\bmod 4)$ and $\lfloor k / r\rfloor \equiv k-b_{k}(\bmod 4)$. We therefore have
$$
m_{k}=i^{k-a_{k}}(-i)^{k-b_{k}}=\left(-i^{2}\right)^{k} i^{-a_{k}}(-i)^{-b_{k}}=(-i)^{a_{k}} i^{b_{k}} .
$$
As $\ell$ and $r$ are relatively prime, by Chinese Remainder Theorem, there is a bijection between pairs $\left(a_{k}, b_{k}\right)=(k(\bmod \ell), k(\bmod r))$ and the numbers $k=0,1,2, \ldots, \ell r-1$. Hence
$$
\sum_{k=0}^{\ell r-1} m_{k}=\sum_{k=0}^{\ell r-1}(-i)^{a_{k}} i^{b_{k}}=\left(\sum_{k=0}^{\ell-1}(-i)^{a_{k}}\right)\left(\sum_{k=0}^{r-1} i^{b_{k}}\right)=1 \times 1=1
$$
as required because $\ell \equiv r \equiv 1(\bmod 4)$.
Case $4 \mathrm{~b}: \underline{\ell \equiv r \equiv 3(\bmod 4)}$. In this case, we get
$$
m_{k}=i^{a_{k}}(-i)^{b_{k}}
$$
where $a_{k}(\equiv k(\bmod \ell))$ and $b_{k}(\equiv k(\bmod r))$ for $k=0,1, \ldots, \ell r-1$. Then we can proceed analogously to Case 4a to obtain
$$
\sum_{k=0}^{\ell r-1} m_{k}=\sum_{k=0}^{\ell r-1}(-i)^{a_{k}} i^{b_{k}}=\left(\sum_{k=0}^{\ell-1}(-i)^{a_{k}}\right)\left(\sum_{k=0}^{r-1} i^{b_{k}}\right)=i \times(-i)=1
$$
as required because $\ell \equiv r \equiv 3(\bmod 4)$.
Now clearly the car traverses through all points between $(0,0)$ and $(1,0)$ during the first section and, in fact, covers all points between $(n-1,0)$ and $(n, 0)$ during the $n$-th section. Hence it will eventually reach $(d, 0)$ for any positive $d$.
To summarize: $(\ell, r)$ satisfies the required conditions if and only if
$$
\ell \equiv r \equiv 1 \quad \text { or } \quad \ell \equiv r \equiv 3 \quad(\bmod 4)
$$
Remark. In case $\operatorname{gcd}(\ell, r)=d \neq 1$, the answer is :
$$
\frac{\ell}{d} \equiv \frac{r}{d} \equiv 1 \quad \text { or } \quad \frac{\ell}{d} \equiv \frac{r}{d} \equiv 3 \quad(\bmod 4)
$$
|
{
"problem_match": "\nProblem 5.",
"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl",
"solution_match": "(Solution)"
}
| 171
| 1,791
|
2010
|
T1
|
3
| null |
APMO
|
Let $n$ be a positive integer. $n$ people take part in a certain party. For any pair of the participants, either the two are acquainted with each other or they are not. What is the maximum possible number of the pairs for which the two are not acquainted but have a common acquaintance among the participants?
|
When 1 participant, say the person $A$, is mutually acquainted with each of the remaining $n-1$ participants, and if there are no other acquaintance relationships among the participants, then for any pair of participants not involving $A$, the two are not mutual acquaintances, but they have a common acquaintance, namely $A$, so any such pair satisfies the requirement. Thus, the number desired in this case is $\frac{(n-1)(n-2)}{2}=\frac{n^{2}-3 n+2}{2}$.
Let us show that $\frac{n^{2}-3 n+2}{2}$ is the maximum possible number of the pairs satisfying the requirement of the problem. First, let us observe that in the process of trying to find the maximum possible number of such pairs, if we split the participants into two non-empty subsets $T$ and $S$ which are disjoint, we may assume that there is a pair consisting of one person chosen from $T$ and the other chosen from $S$ who are mutual acquaintances. This is so, since if there are no such pair for some splitting $T$ and $S$, then among the pairs consisting of one person chosen from $T$ and the other chosen from $S$, there is no pair for which the two have a common acquaintance among participants, and therefore, if we arbitrarily choose a person $A \in T$ and $B \in S$ and declare that $A$ and $B$ are mutual acquaintances, the number of the pairs satisfying the requirement of the problem does not decrease.
Let us now call a set of participants a group if it satisfies the following 2 conditions:
- One can connect any person in the set with any other person in the set by tracing a chain of mutually acquainted pairs. More precisely, for any pair of people $A, B$ in the set there exists a sequence of people $A_{0}, A_{1}, \cdots, A_{n}$ for which $A_{0}=A, A_{n}=B$ and, for each $i: 0 \leq i \leq n-1, A_{i}$ and $A_{i+1}$ are mutual acquaintances.
- No person in this set can be connected with a person not belonging to this set by tracing a chain of mutually acquainted pairs.
In view of the discussions made above, we may assume that the set of all the participants to the party forms a group of $n$ people. Let us next consider the following lemma.
Lemma. In a group of $n$ people, there are at least $n-1$ pairs of mutual acquaintances.
Proof: If you choose a mutually acquainted pair in a group and declare the two in the pair are not mutually acquainted, then either the group stays the same or splits into 2 groups. This means that by changing the status of a mutually acquainted pair in a group to that of a non-acquainted pair, one can increase the number of groups at most by 1 . Now if in a group of $n$ people you change the status of all of the mutually acquainted pairs to that of non-acquainted pairs, then obviously, the number of groups increases from 1 to $n$. Therefore, there must be at least $n-1$ pairs of mutually acquainted pairs in a group consisting of $n$ people.
The lemma implies that there are at most $\frac{n(n-1)}{2}-(n-1)=\frac{n^{2}-3 n+2}{2}$ pairs satisfying the condition of the problem. Thus the desired maximum number of pairs satisfying the requirement of the problem is $\frac{n^{2}-3 n+2}{2}$.
Remark: One can give a somewhat different proof by separating into 2 cases depending on whether there are at least $n-1$ mutually acquainted pairs, or at most $n-2$ such pairs. In the former case, one can argue in the same way as the proof above, while in the latter case, the Lemma above implies that there would be 2 or more groups to start with, but then, in view of the comment made before the definition of a group above, these groups can be combined to form one group, thereby one can reduce the argument to the former case.
Alternate Solution 1: The construction of an example for the case for which the number $\frac{n^{2}-3 n+2}{2}$ appears, and the argument for the case where there is only 1 group would be the same as in the preceding proof.
Suppose, then, $n$ participants are separated into $k(k \geq 2)$ groups, and the number of people in each group is given by $a_{i}, i=1, \cdots, k$. In such a case, the number of pairs for which paired people are not mutually acquainted but have a common acquaintance is at most $\sum_{i=1}^{k} a_{i} C_{2}$, where we set ${ }_{1} C_{2}=0$ for convenience. Since ${ }_{a} C_{2}+{ }_{b} C_{2} \leq{ }_{a+b} C_{2}$ holds for any pair of positive integers $a, b$, we have $\sum_{i=1}^{k} a_{i} C_{2} \leq{ }_{a_{1}} C_{2}+{ }_{n-a_{1}} C_{2}$. From
$$
{ }_{a_{1}} C_{2}+{ }_{n-a_{1}} C_{2}=a_{1}^{2}-n a_{1}+\frac{n^{2}-n}{2}=\left(a_{1}-\frac{n}{2}\right)^{2}+\frac{n^{2}-2 n}{4}
$$
it follows that ${ }_{a} C_{2}+{ }_{n-a_{1}} C_{2}$ takes its maximum value when $a_{1}=1, n-1$. Therefore, we have $\sum_{i=1}^{k}{ }_{a} C_{2} \leq{ }_{n-1} C_{2}$, which shows that in the case where the number of groups are 2 or more, the number of the pairs for which paired people are not mutually acquainted but have a common acquaintance is at most ${ }_{n-1} C_{2}=\frac{n^{2}-3 n+2}{2}$, and hence the desired maximum number of the pairs satisfying the requirement is $\frac{n^{2}-3 n+2}{2}$.
Alternate Solution 2: Construction of an example would be the same as the preceding proof.
For a participant, say $A$, call another participant, say $B$, a familiar face if $A$ and $B$ are not mutually acquainted but they have a common acquaintance among the participants, and in this case call the pair $A, B$ a familiar pair.
Suppose there is a participant $P$ who is mutually acquainted with $d$ participants. Denote by $S$ the set of these $d$ participants, and by $T$ the set of participants different from $P$ and not belonging to the set $S$. Suppose there are $e$ pairs formed by a person in $S$ and a person in $T$ who are mutually acquainted.
Then the number of participants who are familiar faces to $P$ is at most $e$. The number of pairs formed by two people belonging to the set $S$ and are mutually acquainted is at most ${ }_{d} C_{2}$. The number of familiar pairs formed by two people belonging to the set $T$ is at most ${ }_{n-d-1} C_{2}$. Since there are $e$ pairs formed by a person in the set $S$ and a person in the set $T$ who are mutually acquainted (and so the pairs are not familiar pairs), we have at most $d(n-1-d)-e$ familiar pairs formed by a person chosen from $S$ and a person chosen from $T$. Putting these together we conclude that there are at most $e+{ }_{d} C_{2}+{ }_{n-1-d} C_{2}+d(n-1-d)-e$ familiar pairs. Since
$$
e+{ }_{d} C_{2}+{ }_{n-1-d} C_{2}+d(n-1-d)-e=\frac{n^{2}-3 n+2}{2}
$$
the number we seek is at most $\frac{n^{2}-3 n+2}{2}$, and hence this is the desired solution to the problem.
|
{
"problem_match": "\nProblem 3.",
"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl",
"solution_match": "\nSolution:"
}
| 65
| 1,842
|
2010
|
T1
|
4
| null |
APMO
|
Let $A B C$ be an acute triangle satisfying the condition $A B>B C$ and $A C>B C$. Denote by $O$ and $H$ the circumcenter and the orthocenter, respectively, of the triangle $A B C$. Suppose that the circumcircle of the triangle $A H C$ intersects the line $A B$ at $M$ different from $A$, and that the circumcircle of the triangle $A H B$ intersects the line $A C$ at $N$ different from $A$. Prove that the circumcenter of the triangle $M N H$ lies on the line $O H$.
|
In the sequel, we denote $\angle B A C=\alpha, \angle C B A=\beta, \angle A C B=\gamma$. Let $O^{\prime}$ be the circumcenter of the triangle $M N H$. The lengths of line segments starting from the point $H$ will be treated as signed quantities.
Let us denote by $M^{\prime}, N^{\prime}$ the point of intersection of $C H, B H$, respectively, with the circumcircle of the triangle $A B C$ (distinct from $C, B$, respectively.) From the fact that 4 points $A, M, H, C$ lie on the same circle, we see that $\angle M H M^{\prime}=\alpha$ holds. Furthermore, $\angle B M^{\prime} C, \angle B N^{\prime} C$ and $\alpha$ are all subtended by the same arc $\widehat{B C}$ of the circumcircle of the triangle $A B C$ at points on the circle, and therefore, we have $\angle B M^{\prime} C=\alpha$, and $\angle B N^{\prime} C=\alpha$ as well. We also have $\angle A B H=\angle A C N^{\prime}$ as they are subtended by the same $\operatorname{arc} A N^{\prime}$ of the circumcircle of the triangle $A B C$ at points on the circle. Since $H M^{\prime} \perp B M, H N^{\prime} \perp A C$, we conclude that
$$
\angle M^{\prime} H B=90^{\circ}-\angle A B H=90^{\circ}-\angle A C N^{\prime}=\alpha
$$
is valid as well. Putting these facts together, we obtain the fact that the quadrilateral $H B M^{\prime} M$ is a rhombus. In a similar manner, we can conclude that the quadrilateral $H C N^{\prime} N$ is also a rhombus. Since both of these rhombuses are made up of 4 right triangles with an angle of magnitude $\alpha$, we also see that these rhombuses are similar.
Let us denote by $P, Q$ the feet of the perpendicular lines on $H M$ and $H N$, respectively, drawn from the point $O^{\prime}$. Since $O^{\prime}$ is the circumcenter of the triangle $M N H, P, Q$ are respectively, the midpoints of the line segments $H M, H N$. Furthermore, if we denote by $R, S$ the feet of the perpendicular lines on $H M$ and $H N$, respectively, drawn from the point $O$, then since $O$ is the circumcenter of both the triangle $M^{\prime} B C$ and the triangle $N^{\prime} B C$, we see that $R$ is the intersection point of $H M$ and the perpendicular bisector of $B M^{\prime}$, and $S$ is the intersection point of $H N$ and the perpendicular bisector of $C N^{\prime}$.
We note that the similarity map $\phi$ between the rhombuses $H B M^{\prime} M$ and $H C N^{\prime} N$ carries the perpendicular bisector of $B M^{\prime}$ onto the perpendicular bisector of $C N^{\prime}$, and straight line $H M$ onto the straight line $H N$, and hence $\phi$ maps $R$ onto $S$, and $P$ onto $Q$. Therefore, we get $H P: H R=H Q: H S$. If we now denote by $X, Y$ the intersection points of the line $H O^{\prime}$ with the line through $R$ and perpendicular to $H P$, and with the line through $S$ and perpendicular to $H Q$, respectively, then we get
$$
H O^{\prime}: H X=H P: H R=H Q: H S=H O^{\prime}: H Y
$$
so that we must have $H X=H Y$, and therefore, $X=Y$. But it is obvious that the point of intersection of the line through $R$ and perpendicular to $H P$ with the line through $S$ and perpendicular to $H Q$ must be $O$, and therefore, we conclude that $X=Y=O$ and that the points $H, O^{\prime}, O$ are collinear.
Alternate Solution: Deduction of the fact that both of the quadrilaterals $H B M^{\prime} M$ and $H C N^{\prime} N$ are rhombuses is carried out in the same way as in the preceding proof.
We then see that the point $M$ is located in a symmetric position with the point $B$ with respect to the line $C H$, we conclude that we have $\angle C M B=\beta$. Similarly, we have $\angle C N B=\gamma$. If we now put $x=\angle A H O^{\prime}$, then we get
$$
\angle O^{\prime}=\beta-\alpha-x, \angle M N H=90^{\circ}-\beta-\alpha+x
$$
from which it follows that
$$
\angle A N M=180^{\circ}-\angle M N H-\left(90^{\circ}-\alpha\right)=\beta-x
$$
Similarly, we get
$$
\angle N M A=\gamma+x
$$
Using the laws of sines, we then get
$$
\begin{aligned}
\frac{\sin (\gamma+x)}{\sin (\beta-x)} & =\frac{A N}{A M}=\frac{A C}{A M} \cdot \frac{A B}{A C} \cdot \frac{A N}{A B} \\
& =\frac{\sin \beta}{\sin (\beta-\alpha)} \cdot \frac{\sin \gamma}{\sin \beta} \cdot \frac{\sin (\gamma-\alpha)}{\sin \gamma}=\frac{\sin (\gamma-\alpha)}{\sin (\beta-\alpha)}
\end{aligned}
$$
On the other hand, if we let $y=\angle A H O$, we then get
$$
\angle O H B=180^{\circ}-\gamma-y, \angle C H O=180^{\circ}-\beta+y,
$$
and since
$$
\angle H B O=\gamma-\alpha, \angle O C H=\beta-\alpha,
$$
using the laws of sines and observing that $O B=O C$, we get
$$
\begin{aligned}
\frac{\sin (\gamma-\alpha)}{\sin (\beta-\alpha)}=\frac{\sin \angle H B O}{\sin \angle O C H} & =\frac{\sin \left(180^{\circ}-\gamma-y\right) \cdot \frac{O H}{O B}}{\sin \left(180^{\circ}-\beta+y\right) \cdot \frac{O H}{O C}} \\
& =\frac{\sin \left(180^{\circ}-\gamma-y\right)}{\sin \left(180^{\circ}-\beta+y\right)}=\frac{\sin (\gamma+y)}{\sin (\beta-y)}
\end{aligned}
$$
We then get $\sin (\gamma+x) \sin (\beta-y)=\sin (\beta-x) \sin (\gamma+y)$. Expanding both sides of the last identity by using the addition formula for the sine function and after factoring and using again the addition formula we obtain that $\sin (x-y) \sin (\beta+\gamma)=0$. This implies that $x-y$ must be an integral multiple of $180^{\circ}$, and hence we conclude that $H, O, O^{\prime}$ are collinear.
|
{
"problem_match": "\nProblem 4.",
"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl",
"solution_match": "\nSolution:"
}
| 135
| 1,732
|
2010
|
T1
|
5
| null |
APMO
|
Find all functions $f$ from the set $\mathbf{R}$ of real numbers into $\mathbf{R}$ which satisfy for all $x, y, z \in \mathbf{R}$ the identity
$$
f(f(x)+f(y)+f(z))=f(f(x)-f(y))+f(2 x y+f(z))+2 f(x z-y z) .
$$
|
It is clear that if $f$ is a constant function which satisfies the given equation, then the constant must be 0 . Conversely, $f(x)=0$ clearly satisfies the given equation, so, the identically 0 function is a solution. In the sequel, we consider the case where $f$ is not a constant function.
Let $t \in \mathbf{R}$ and substitute $(x, y, z)=(t, 0,0)$ and $(x, y, z)=(0, t, 0)$ into the given functional equation. Then, we obtain, respectively,
$$
\begin{aligned}
& f(f(t)+2 f(0))=f(f(t)-f(0))+f(f(0))+2 f(0), \\
& f(f(t)+2 f(0))=f(f(0)-f(t))+f(f(0))+2 f(0)
\end{aligned}
$$
from which we conclude that $f(f(t)-f(0))=f(f(0)-f(t))$ holds for all $t \in \mathbf{R}$. Now, suppose for some pair $u_{1}, u_{2}, f\left(u_{1}\right)=f\left(u_{2}\right)$ is satisfied. Then by substituting $(x, y, z)=\left(s, 0, u_{1}\right)$ and $(x, y, z)=\left(s, 0, u_{2}\right)$ into the functional equation and comparing the resulting identities, we can easily conclude that
$$
f\left(s u_{1}\right)=f\left(s u_{2}\right)
$$
holds for all $s \in \mathbf{R}$. Since $f$ is not a constant function there exists an $s_{0}$ such that $f\left(s_{0}\right)-f(0) \neq$ 0 . If we put $u_{1}=f\left(s_{0}\right)-f(0), u_{2}=-u_{1}$, then $f\left(u_{1}\right)=f\left(u_{2}\right)$, so we have by $(*)$
$$
f\left(s u_{1}\right)=f\left(s u_{2}\right)=f\left(-s u_{1}\right)
$$
for all $s \in \mathbf{R}$. Since $u_{1} \neq 0$, we conclude that
$$
f(x)=f(-x)
$$
holds for all $x \in \mathbf{R}$.
Next, if $f(u)=f(0)$ for some $u \neq 0$, then by $(*)$, we have $f(s u)=f(s 0)=f(0)$ for all $s$, which implies that $f$ is a constant function, contradicting our assumption. Therefore, we must have $f(s) \neq f(0)$ whenever $s \neq 0$.
We will now show that if $f(x)=f(y)$ holds, then either $x=y$ or $x=-y$ must hold. Suppose on the contrary that $f\left(x_{0}\right)=f\left(y_{0}\right)$ holds for some pair of non-zero numbers $x_{0}, y_{0}$ for which $x_{0} \neq y_{0}, x_{0} \neq-y_{0}$. Since $f\left(-y_{0}\right)=f\left(y_{0}\right)$, we may assume, by replacing $y_{0}$ by $-y_{0}$ if necessary, that $x_{0}$ and $y_{0}$ have the same sign. In view of $(*)$, we see that $f\left(s x_{0}\right)=f\left(s y_{0}\right)$ holds for all $s$, and therefore, there exists some $r>0, r \neq 1$ such that
$$
f(x)=f(r x)
$$
holds for all $x$. Replacing $x$ by $r x$ and $y$ by $r y$ in the given functional equation, we obtain
$$
f(f(r x)+f(r y)+f(z))=f(f(r x)-f(r y))+f\left(2 r^{2} x y+f(z)\right)+2 f(r(x-y) z)
$$
and replacing $x$ by $r^{2} x$ in the functional equation, we get
$$
f\left(f\left(r^{2} x\right)+f(y)+f(z)\right)=f\left(f\left(r^{2} x\right)-f(y)\right)+f\left(2 r^{2} x y+f(z)\right)+2 f\left(\left(r^{2} x-y\right) z\right)
$$
Since $f(r x)=f(x)$ holds for all $x \in \mathbf{R}$, we see that except for the last term on the right-hand side, all the corresponding terms appearing in the identities (i) and (ii) above are equal, and hence we conclude that
$$
\left.f(r(x-y) z)=f\left(\left(r^{2} x-y\right) z\right)\right)
$$
must hold for arbitrary choice of $x, y, z \in \mathbf{R}$. For arbitrarily fixed pair $u, v \in \mathbf{R}$, substitute $(x, y, z)=\left(\frac{v-u}{r^{2}-1}, \frac{v-r^{2} u}{r^{2}-1}, 1\right)$ into the identity (iii). Then we obtain $f(v)=f(r u)=f(u)$, since $x-y=u, r^{2} x-y=v, z=1$. But this implies that the function $f$ is a constant, contradicting our assumption. Thus we conclude that if $f(x)=f(y)$ then either $x=y$ or $x=-y$ must hold.
By substituting $z=0$ in the functional equation, we get
$$
f(f(x)+f(y)+f(0))=f(f(x)-f(y)+f(0))=f((f(x)-f(y))+f(2 x y+f(0))+2 f(0)
$$
Changing $y$ to $-y$ in the identity above and using the fact that $f(y)=f(-y)$, we see that all the terms except the second term on the right-hand side in the identity above remain the same. Thus we conclude that $f(2 x y+f(0))=f(-2 x y+f(0))$, from which we get either $2 x y+f(0)=-2 x y+f(0)$ or $2 x y+f(0)=2 x y-f(0)$ for all $x, y \in \mathbf{R}$. The first of these alternatives says that $4 x y=0$, which is impossible if $x y \neq 0$. Therefore the second alternative must be valid and we get that $f(0)=0$.
Finally, let us show that if $f$ satisfies the given functional equation and is not a constant function, then $f(x)=x^{2}$. Let $x=y$ in the functional equation, then since $f(0)=0$, we get
$$
f(2 f(x)+f(z))=f\left(2 x^{2}+f(z)\right)
$$
from which we conclude that either $2 f(x)+f(z)=2 x^{2}+f(z)$ or $2 f(x)+f(z)=-2 x^{2}-f(z)$ must hold. Suppose there exists $x_{0}$ for which $f\left(x_{0}\right) \neq x_{0}^{2}$, then from the second alternative, we see that $f(z)=-f\left(x_{0}\right)-x_{0}^{2}$ must hold for all $z$, which means that $f$ must be a constant function, contrary to our assumption. Therefore, the first alternative above must hold, and we have $f(x)=x^{2}$ for all $x$, establishing our claim.
It is easy to check that $f(x)=x^{2}$ does satisfy the given functional equation, so we conclude that $f(x)=0$ and $f(x)=x^{2}$ are the only functions that satisfy the requirement.
|
{
"problem_match": "\nProblem 5.",
"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl",
"solution_match": "\nSolution:"
}
| 83
| 1,847
|
2013
|
T1
|
1
| null |
APMO
|
Let $A B C$ be an acute triangle with altitudes $A D, B E$ and $C F$, and let $O$ be the center of its circumcircle. Show that the segments $O A, O F, O B, O D, O C, O E$ dissect the triangle $A B C$ into three pairs of triangles that have equal areas.
|
Let $M$ and $N$ be midpoints of sides $B C$ and $A C$, respectively. Notice that $\angle M O C=\frac{1}{2} \angle B O C=\angle E A B, \angle O M C=90^{\circ}=\angle A E B$, so triangles $O M C$ and $A E B$ are similar and we get $\frac{O M}{A E}=\frac{O C}{A B}$. For triangles $O N A$ and $B D A$ we also have $\frac{O N}{B D}=\frac{O A}{B A}$. Then $\frac{O M}{A E}=\frac{O N}{B D}$ or $B D \cdot O M=A E \cdot O N$.
Denote by $S(\Phi)$ the area of the figure $\Phi$. So, we see that $S(O B D)=\frac{1}{2} B D \cdot O M=$ $\frac{1}{2} A E \cdot O N=S(O A E)$. Analogously, $S(O C D)=S(O A F)$ and $S(O C E)=S(O B F)$.
Alternative solution. Let $R$ be the circumradius of triangle $A B C$, and as usual write $A, B, C$ for angles $\angle C A B, \angle A B C, \angle B C A$ respectively, and $a, b, c$ for sides $B C, C A, A B$ respectively. Then the area of triangle $O C D$ is
$$
S(O C D)=\frac{1}{2} \cdot O C \cdot C D \cdot \sin (\angle O C D)=\frac{1}{2} R \cdot C D \cdot \sin (\angle O C D)
$$
Now $C D=b \cos C$, and
$$
\angle O C D=\frac{180^{\circ}-2 A}{2}=90^{\circ}-A
$$
(since triangle $O B C$ is isosceles, and $\angle B O C=2 A$ ). So
$$
S(O C D)=\frac{1}{2} R b \cos C \sin \left(90^{\circ}-A\right)=\frac{1}{2} R b \cos C \cos A
$$
A similar calculation gives
$$
\begin{aligned}
S(O A F) & =\frac{1}{2} O A \cdot A F \cdot \sin (\angle O A F) \\
& =\frac{1}{2} R \cdot(b \cos A) \sin \left(90^{\circ}-C\right) \\
& =\frac{1}{2} R b \cos A \cos C
\end{aligned}
$$
so $O C D$ and $O A F$ have the same area. In the same way we find that $O B D$ and $O A E$ have the same area, as do $O C E$ and $O B F$.
|
{
"problem_match": "\nProblem 1.",
"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl",
"solution_match": "\nSolution."
}
| 79
| 678
|
2013
|
T1
|
2
| null |
APMO
|
Determine all positive integers $n$ for which $\frac{n^{2}+1}{[\sqrt{n}]^{2}+2}$ is an integer. Here $[r]$ denotes the greatest integer less than or equal to $r$.
|
We will show that there are no positive integers $n$ satisfying the condition of the problem.
Let $m=[\sqrt{n}]$ and $a=n-m^{2}$. We have $m \geq 1$ since $n \geq 1$. From $n^{2}+1=\left(m^{2}+a\right)^{2}+1 \equiv$ $(a-2)^{2}+1\left(\bmod \left(m^{2}+2\right)\right)$, it follows that the condition of the problem is equivalent to the fact that $(a-2)^{2}+1$ is divisible by $m^{2}+2$. Since we have
$$
0<(a-2)^{2}+1 \leq \max \left\{2^{2},(2 m-2)^{2}\right\}+1 \leq 4 m^{2}+1<4\left(m^{2}+2\right)
$$
we see that $(a-2)^{2}+1=k\left(m^{2}+2\right)$ must hold with $k=1,2$ or 3 . We will show that none of these can occur.
Case 1. When $k=1$. We get $(a-2)^{2}-m^{2}=1$, and this implies that $a-2= \pm 1, m=0$ must hold, but this contradicts with fact $m \geq 1$.
Case 2. When $k=2$. We have $(a-2)^{2}+1=2\left(m^{2}+2\right)$ in this case, but any perfect square is congruent to $0,1,4 \bmod 8$, and therefore, we have $(a-2)^{2}+1 \equiv 1,2,5(\bmod 8)$, while $2\left(m^{2}+2\right) \equiv 4,6(\bmod 8)$. Thus, this case cannot occur either.
Case 3. When $k=3$. We have $(a-2)^{2}+1=3\left(m^{2}+2\right)$ in this case. Since any perfect square is congruent to 0 or $1 \bmod 3$, we have $(a-2)^{2}+1 \equiv 1,2(\bmod 3)$, while $3\left(m^{2}+2\right) \equiv 0$ $(\bmod 3)$, which shows that this case cannot occur either.
|
{
"problem_match": "\nProblem 2.",
"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl",
"solution_match": "\nSolution."
}
| 50
| 572
|
2013
|
T1
|
4
| null |
APMO
|
Let $a$ and $b$ be positive integers, and let $A$ and $B$ be finite sets of integers satisfying:
(i) $A$ and $B$ are disjoint;
(ii) if an integer $i$ belongs either to $A$ or to $B$, then $i+a$ belongs to $A$ or $i-b$ belongs to $B$.
Prove that $a|A|=b|B|$. (Here $|X|$ denotes the number of elements in the set $X$.)
|
Let $A^{*}=\{n-a: n \in A\}$ and $B^{*}=\{n+b: n \in B\}$. Then, by (ii), $A \cup B \subseteq A^{*} \cup B^{*}$ and by (i),
$$
|A \cup B| \leq\left|A^{*} \cup B^{*}\right| \leq\left|A^{*}\right|+\left|B^{*}\right|=|A|+|B|=|A \cup B|
$$
Thus, $A \cup B=A^{*} \cup B^{*}$ and $A^{*}$ and $B^{*}$ have no element in common. For each finite set $X$ of integers, let $\sum(X)=\sum_{x \in X} x$. Then
$$
\begin{aligned}
\sum(A)+\sum(B) & =\sum(A \cup B) \\
& =\sum\left(A^{*} \cup B^{*}\right)=\sum\left(A^{*}\right)+\sum\left(B^{*}\right) \\
& =\sum(A)-a|A|+\sum(B)+b|B|
\end{aligned}
$$
which implies $a|A|=b|B|$.
Alternative solution. Let us construct a directed graph whose vertices are labelled by the members of $A \cup B$ and such that there is an edge from $i$ to $j$ iff $j \in A$ and $j=i+a$ or $j \in B$ and $j=i-b$. From (ii), each vertex has out-degree $\geq 1$ and, from (i), each vertex has in-degree $\leq 1$. Since the sum of the out-degrees equals the sum of the in-degrees, each vertex has in-degree and out-degree equal to 1. This is only possible if the graph is the union of disjoint cycles, say $G_{1}, G_{2}, \ldots, G_{n}$. Let $\left|A_{k}\right|$ be the number of elements of $A$ in $G_{k}$ and $\left|B_{k}\right|$ be the number of elements of $B$ in $G_{k}$. The cycle $G_{k}$ will involve increasing vertex labels by $a$ a total of $\left|A_{k}\right|$ times and decreasing them by $b$ a total of $\left|B_{k}\right|$ times. Since it is a cycle, we have $a\left|A_{k}\right|=b\left|B_{k}\right|$. Summing over all cycles gives the result.
|
{
"problem_match": "\nProblem 4.",
"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl",
"solution_match": "\nSolution."
}
| 111
| 589
|
2013
|
T1
|
5
| null |
APMO
|
Let $A B C D$ be a quadrilateral inscribed in a circle $\omega$, and let $P$ be a point on the extension of $A C$ such that $P B$ and $P D$ are tangent to $\omega$. The tangent at $C$ intersects $P D$ at $Q$ and the line $A D$ at $R$. Let $E$ be the second point of intersection between $A Q$ and $\omega$. Prove that $B, E, R$ are collinear.
|
To show $B, E, R$ are collinear, it is equivalent to show the lines $A D, B E, C Q$ are concurrent. Let $C Q$ intersect $A D$ at $R$ and $B E$ intersect $A D$ at $R^{\prime}$. We shall show $R D / R A=R^{\prime} D / R^{\prime} A$ so that $R=R^{\prime}$.
Since $\triangle P A D$ is similar to $\triangle P D C$ and $\triangle P A B$ is similar to $\triangle P B C$, we have $A D / D C=$ $P A / P D=P A / P B=A B / B C$. Hence, $A B \cdot D C=B C \cdot A D$. By Ptolemy's theorem, $A B \cdot D C=B C \cdot A D=\frac{1}{2} C A \cdot D B$. Similarly $C A \cdot E D=C E \cdot A D=\frac{1}{2} A E \cdot D C$.
Thus
$$
\frac{D B}{A B}=\frac{2 D C}{C A}
$$
and
$$
\frac{D C}{C A}=\frac{2 E D}{A E}
$$
Since the triangles $R D C$ and $R C A$ are similar, we have $\frac{R D}{R C}=\frac{D C}{C A}=\frac{R C}{R A}$. Thus using (4)
$$
\frac{R D}{R A}=\frac{R D \cdot R A}{R A^{2}}=\left(\frac{R C}{R A}\right)^{2}=\left(\frac{D C}{C A}\right)^{2}=\left(\frac{2 E D}{A E}\right)^{2}
$$
Using the similar triangles $A B R^{\prime}$ and $E D R^{\prime}$, we have $R^{\prime} D / R^{\prime} B=E D / A B$. Using the similar triangles $D B R^{\prime}$ and $E A R^{\prime}$ we have $R^{\prime} A / R^{\prime} B=E A / D B$. Thus using (3) and (4),
$$
\frac{R^{\prime} D}{R^{\prime} A}=\frac{E D \cdot D B}{E A \cdot A B}=\left(\frac{2 E D}{A E}\right)^{2}
$$
It follows from (5) and (6) that $R=R^{\prime}$.
|
{
"problem_match": "\nProblem 5.",
"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl",
"solution_match": "\nSolution."
}
| 111
| 585
|
2014
|
T1
|
2
| null |
APMO
|
Let $S=\{1,2, \ldots, 2014\}$. For each non-empty subset $T \subseteq S$, one of its members is chosen as its representative. Find the number of ways to assign representatives to all non-empty subsets of $S$ so that if a subset $D \subseteq S$ is a disjoint union of non-empty subsets $A, B, C \subseteq S$, then the representative of $D$ is also the representative of at least one of $A, B, C$. (Warut Suksompong, Thailand)
|
Answer: 108 - 2014!.
For any subset $X$ let $r(X)$ denotes the representative of $X$. Suppose that $x_{1}=r(S)$. First, we prove the following fact:
$$
\text { If } x_{1} \in X \text { and } X \subseteq S \text {, then } x_{1}=r(X) \text {. }
$$
If $|X| \leq 2012$, then we can write $S$ as a disjoint union of $X$ and two other subsets of $S$, which gives that $x_{1}=r(X)$. If $|X|=2013$, then let $y \in X$ and $y \neq x_{1}$. We can write $X$ as a disjoint union of $\left\{x_{1}, y\right\}$ and two other subsets. We already proved that $r\left(\left\{x_{1}, y\right\}\right)=x_{1}$ (since $\left|\left\{x_{1}, y\right\}\right|=2<2012$ ) and it follows that $y \neq r(X)$ for every $y \in X$ except $x_{1}$. We have proved the fact.
Note that this fact is true and can be proved similarly, if the ground set $S$ would contain at least 5 elements.
There are 2014 ways to choose $x_{1}=r(S)$ and for $x_{1} \in X \subseteq S$ we have $r(X)=x_{1}$. Let $S_{1}=S \backslash\left\{x_{1}\right\}$. Analogously, we can state that there are 2013 ways to choose $x_{2}=r\left(S_{1}\right)$ and for $x_{2} \in X \subseteq S_{1}$ we have $r(X)=x_{2}$. Proceeding similarly (or by induction), there are $2014 \cdot 2013 \cdots 5$ ways to choose $x_{1}, x_{2}, \ldots, x_{2010} \in S$ so that for all $i=1,2 \ldots, 2010$, $x_{i}=r(X)$ for each $X \subseteq S \backslash\left\{x_{1}, \ldots, x_{i-1}\right\}$ and $x_{i} \in X$.
We are now left with four elements $Y=\left\{y_{1}, y_{2}, y_{3}, y_{4}\right\}$. There are 4 ways to choose $r(Y)$. Suppose that $y_{1}=r(Y)$. Then we clearly have $y_{1}=r\left(\left\{y_{1}, y_{2}\right\}\right)=r\left(\left\{y_{1}, y_{3}\right\}\right)=r\left(\left\{y_{1}, y_{4}\right\}\right)$. The only subsets whose representative has not been assigned yet are $\left\{y_{1}, y_{2}, y_{3}\right\},\left\{y_{1}, y_{2}, y_{4}\right\}$, $\left\{y_{1}, y_{3}, y_{4}\right\},\left\{y_{2}, y_{3}, y_{4}\right\},\left\{y_{2}, y_{3}\right\},\left\{y_{2}, y_{4}\right\},\left\{y_{3}, y_{4}\right\}$. These subsets can be assigned in any way, hence giving $3^{4} \cdot 2^{3}$ more choices.
In conclusion, the total number of assignments is $2014 \cdot 2013 \cdots 4 \cdot 3^{4} \cdot 2^{3}=108 \cdot 2014$ !.
|
{
"problem_match": "\nProblem 2.",
"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl",
"solution_match": "\nSolution."
}
| 121
| 901
|
2014
|
T1
|
4
| null |
APMO
|
Let $n$ and $b$ be positive integers. We say $n$ is $b$-discerning if there exists a set consisting of $n$ different positive integers less than $b$ that has no two different subsets $U$ and $V$ such that the sum of all elements in $U$ equals the sum of all elements in $V$.
(a) Prove that 8 is a 100 -discerning.
(b) Prove that 9 is not 100-discerning.
(Senior Problems Committee of the Australian Mathematical Olympiad Committee)
|
(a) Take $S=\{3,6,12,24,48,95,96,97\}$, i.e.
$$
S=\left\{3 \cdot 2^{k}: 0 \leq k \leq 5\right\} \cup\left\{3 \cdot 2^{5}-1,3 \cdot 2^{5}+1\right\}
$$
As $k$ ranges between 0 to 5 , the sums obtained from the numbers $3 \cdot 2^{k}$ are $3 t$, where $1 \leq t \leq 63$. These are 63 numbers that are divisible by 3 and are at most $3 \cdot 63=189$.
Sums of elements of $S$ are also the numbers $95+97=192$ and all the numbers that are sums of 192 and sums obtained from the numbers $3 \cdot 2^{k}$ with $0 \leq k \leq 5$. These are 64 numbers that are all divisible by 3 and at least equal to 192. In addition, sums of elements of $S$ are the numbers 95 and all the numbers that are sums of 95 and sums obtained from the numbers $3 \cdot 2^{k}$ with $0 \leq k \leq 5$. These are 64 numbers that are all congruent to $-1 \bmod$ 3.
Finally, sums of elements of $S$ are the numbers 97 and all the numbers that are sums of 97 and sums obtained from the numbers $3 \cdot 2^{k}$ with $0 \leq k \leq 5$. These are 64 numbers that are all congruent to $1 \bmod 3$.
Hence there are at least $63+64+64+64=255$ different sums from elements of $S$. On the other hand, $S$ has $2^{8}-1=255$ non-empty subsets. Therefore $S$ has no two different subsets with equal sums of elements. Therefore, 8 is 100 -discerning.
(b) Suppose that 9 is 100 -discerning. Then there is a set $S=\left\{s_{1}, \ldots, s_{9}\right\}, s_{i}<100$ that has no two different subsets with equal sums of elements. Assume that $0<s_{1}<\cdots<s_{9}<$ 100.
Let $X$ be the set of all subsets of $S$ having at least 3 and at most 6 elements and let $Y$ be the set of all subsets of $S$ having exactly 2 or 3 or 4 elements greater than $s_{3}$.
The set $X$ consists of
$$
\binom{9}{3}+\binom{9}{4}+\binom{9}{5}+\binom{9}{6}=84+126+126+84=420
$$
subsets of $S$. The set in $X$ with the largest sums of elements is $\left\{s_{4}, \ldots, s_{9}\right\}$ and the smallest sums is in $\left\{s_{1}, s_{2}, s_{3}\right\}$. Thus the sum of the elements of each of the 420 sets in $X$ is at least $s_{1}+s_{2}+s_{3}$ and at most $s_{4}+\cdots+s_{9}$, which is one of $\left(s_{4}+\cdots+s_{9}\right)-\left(s_{1}+s_{2}+s_{3}\right)+1$ integers. From the pigeonhole principle it follows that $\left(s_{4}+\cdots+s_{9}\right)-\left(s_{1}+s_{2}+s_{3}\right)+1 \geq 420$, i.e.,
$$
\left(s_{4}+\cdots+s_{9}\right)-\left(s_{1}+s_{2}+s_{3}\right) \geq 419
$$
Now let us calculate the number of subsets in $Y$. Observe that $\left\{s_{4}, \ldots, s_{9}\right\}$ has $\binom{6}{2}$ 2-element subsets, $\binom{6}{3}$ 3-element subsets and $\binom{6}{4}$ 4-element subsets, while $\left\{s_{1}, s_{2}, s_{3}\right\}$ has exactly 8 subsets. Hence the number of subsets of $S$ in $Y$ equals
$$
8\left(\binom{6}{2}+\binom{6}{3}+\binom{6}{4}\right)=8(15+20+15)=400
$$
The set in $Y$ with the largest sum of elements is $\left\{s_{1}, s_{2}, s_{3}, s_{6}, s_{7}, s_{8}, s_{9}\right\}$ and the smallest sum is in $\left\{s_{4}, s_{5}\right\}$. Again, by the pigeonhole principle it follows that $\left(s_{1}+s_{2}+s_{3}+s_{6}+s_{7}+\right.$ $\left.s_{8}+s_{9}\right)-\left(s_{4}+s_{5}\right)+1 \geq 400$, i.e.,
$$
\left(s_{1}+s_{2}+s_{3}+s_{6}+s_{7}+s_{8}+s_{9}\right)-\left(s_{4}+s_{5}\right) \geq 399
$$
Adding (1) and (2) yields $2\left(s_{6}+s_{7}+s_{8}+s_{9}\right) \geq 818$, so that $s_{9}+98+97+96 \geq$ $s_{9}+s_{8}+s_{7}+s_{6} \geq 409$, i.e. $s_{9} \geq 118$, a contradiction with $s_{9}<100$. Therefore, 9 is not 100-discerning.
|
{
"problem_match": "\nProblem 4.",
"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl",
"solution_match": "# Solution."
}
| 126
| 1,460
|
2014
|
T1
|
5
| null |
APMO
|
Circles $\omega$ and $\Omega$ meet at points $A$ and $B$. Let $M$ be the midpoint of the $\operatorname{arc} A B$ of circle $\omega$ ( $M$ lies inside $\Omega$ ). A chord $M P$ of circle $\omega$ intersects $\Omega$ at $Q(Q$ lies inside $\omega)$. Let $\ell_{P}$ be the tangent line to $\omega$ at $P$, and let $\ell_{Q}$ be the tangent line to $\Omega$ at $Q$. Prove that the circumcircle of the triangle formed by the lines $\ell_{P}, \ell_{Q}$, and $A B$ is tangent to $\Omega$. (Ilya Bogdanov, Russia and Medeubek Kungozhin, Kazakhstan)
|
Denote $X=A B \cap \ell_{P}, Y=A B \cap \ell_{Q}$, and $Z=\ell_{P} \cap \ell_{Q}$. Without loss of generality we have $A X<B X$. Let $F=M P \cap A B$.
Denote by $R$ the second point of intersection of $P Q$ and $\Omega$; by $S$ the point of $\Omega$ such that $S R \| A B$; and by $T$ the point of $\Omega$ such that $R T \| \ell_{P}$. Since $M$ is the midpoint of arc $A B$, the tangent $\ell_{M}$ at $M$ to $\omega$ is parallel to $A B$, so $\angle(A B, P M)=\angle\left(P M, \ell_{P}\right)$. Therefore we have $\angle P R T=\angle M P X=\angle P F X=\angle P R S$. Thus the point $Q$ is the midpoint of the $\operatorname{arc} T Q S$ of $\Omega$, hence $S T \| \ell_{Q}$. So the corresponding sides of the triangles $R S T$ and $X Y Z$ are parallel, and there exist a homothety $h$ mapping $R S T$ to $X Y Z$.
Let $D$ be the second point of intersection of $X R$ and $\Omega$. We claim that $D$ is the center of the homothety $h$; since $D \in \Omega$, this implies that the circumcircles of triangles $R S T$ and $X Y Z$ are tangent, as required. So, it remains to prove this claim. In order to do this, it suffices to show that $D \in S Y$.
By $\angle P F X=\angle X P F$ we have $X F^{2}=X P^{2}=X A \cdot X B=X D \cdot X R$. Therefore, $\frac{X F}{X D}=\frac{X R}{X F}$, so the triangles $X D F$ and $X F R$ are similar, hence $\angle D F X=\angle X R F=\angle D R Q=$ $\angle D Q Y$; thus the points $D, Y, Q$, and $F$ are concyclic. It follows that $\angle Y D Q=\angle Y F Q=$ $\angle S R Q=180^{\circ}-\angle S D Q$ which means exactly that the points $Y, D$, and $S$ are collinear, with $D$ between $S$ and $Y$.
|
{
"problem_match": "\nProblem 5.",
"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl",
"solution_match": "\nSolution."
}
| 170
| 573
|
2015
|
T1
|
1
| null |
APMO
|
Let $A B C$ be a triangle, and let $D$ be a point on side $B C$. A line through $D$ intersects side $A B$ at $X$ and ray $A C$ at $Y$. The circumcircle of triangle $B X D$ intersects the circumcircle $\omega$ of triangle $A B C$ again at point $Z \neq B$. The lines $Z D$ and $Z Y$ intersect $\omega$ again at $V$ and $W$, respectively. Prove that $A B=V W$.
|
Suppose $X Y$ intersects $\omega$ at points $P$ and $Q$, where $Q$ lies between $X$ and $Y$. We will show that $V$ and $W$ are the reflections of $A$ and $B$ with respect to the perpendicular bisector of $P Q$. From this, it follows that $A V W B$ is an isosceles trapezoid and hence $A B=V W$.
First, note that
$$
\angle B Z D=\angle A X Y=\angle A P Q+\angle B A P=\angle A P Q+\angle B Z P,
$$
so $\angle A P Q=\angle P Z V=\angle P Q V$, and hence $V$ is the reflection of $A$ with respect to the perpendicular bisector of $P Q$.
Now, suppose $W^{\prime}$ is the reflection of $B$ with respect to the perpendicular bisector of $P Q$, and let $Z^{\prime}$ be the intersection of $Y W^{\prime}$ and $\omega$. It suffices to show that $B, X, D, Z^{\prime}$ are concyclic. Note that
$$
\angle Y D C=\angle P D B=\angle P C B+\angle Q P C=\angle W^{\prime} P Q+\angle Q P C=\angle W^{\prime} P C=\angle Y Z^{\prime} C .
$$
So $D, C, Y, Z^{\prime}$ are concyclic. Next, $\angle B Z^{\prime} D=\angle C Z^{\prime} B-\angle C Z^{\prime} D=180^{\circ}-\angle B X D$ and due to the previous concyclicity we are done.
Alternative solution 1. Using cyclic quadrilaterals $B X D Z$ and $A B Z V$ in turn, we have $\angle Z D Y=\angle Z B A=\angle Z C Y$. So $Z D C Y$ is cyclic.
Using cyclic quadrilaterals $A B Z C$ and $Z D C Y$ in turn, we have $\angle A Z B=\angle A C B=\angle W Z V$ (or $180^{\circ}-\angle W Z V$ if $Z$ lies between $W$ and $C$ ).
So $A B=V W$ because they subtend equal (or supplementary) angles in $\omega$.
Alternative solution 2. Using cyclic quadrilaterals $B X D Z$ and $A B Z V$ in turn, we have $\angle Z D Y=\angle Z B A=\angle Z C Y$. So $Z D C Y$ is cyclic.
Using cyclic quadrilaterals $B X D Z$ and $A B Z V$ in turn, we have $\angle D X A=\angle V Z B=$ $180^{\circ}-B A V$. So $X D \| A V$.
Using cyclic quadrilaterals $Z D C Y$ and $B C W Z$ in turn, we have $\angle Y D C=\angle Y Z C=$ $\angle W B C$. So $X D \| B W$.
Hence $B W \| A V$ which implies that $A V W B$ is an isosceles trapezium with $A B=V W$.
|
{
"problem_match": "\nProblem 1.",
"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl",
"solution_match": "\nSolution."
}
| 120
| 725
|
2015
|
T1
|
2
| null |
APMO
|
Let $S=\{2,3,4, \ldots\}$ denote the set of integers that are greater than or equal to 2 . Does there exist a function $f: S \rightarrow S$ such that
$$
f(a) f(b)=f\left(a^{2} b^{2}\right) \text { for all } a, b \in S \text { with } a \neq b ?
$$
|
We prove that there is no such function. For arbitrary elements $a$ and $b$ of $S$, choose an integer $c$ that is greater than both of them. Since $b c>a$ and $c>b$, we have
$$
f\left(a^{4} b^{4} c^{4}\right)=f\left(a^{2}\right) f\left(b^{2} c^{2}\right)=f\left(a^{2}\right) f(b) f(c)
$$
Furthermore, since $a c>b$ and $c>a$, we have
$$
f\left(a^{4} b^{4} c^{4}\right)=f\left(b^{2}\right) f\left(a^{2} c^{2}\right)=f\left(b^{2}\right) f(a) f(c)
$$
Comparing these two equations, we find that for all elements $a$ and $b$ of $S$,
$$
f\left(a^{2}\right) f(b)=f\left(b^{2}\right) f(a) \quad \Longrightarrow \quad \frac{f\left(a^{2}\right)}{f(a)}=\frac{f\left(b^{2}\right)}{f(b)} .
$$
It follows that there exists a positive rational number $k$ such that
$$
f\left(a^{2}\right)=k f(a), \quad \text { for all } a \in S
$$
Substituting this into the functional equation yields
$$
f(a b)=\frac{f(a) f(b)}{k}, \quad \text { for all } a, b \in S \text { with } a \neq b .
$$
Now combine the functional equation with equations (1) and (2) to obtain
$$
f(a) f\left(a^{2}\right)=f\left(a^{6}\right)=\frac{f(a) f\left(a^{5}\right)}{k}=\frac{f(a) f(a) f\left(a^{4}\right)}{k^{2}}=\frac{f(a) f(a) f\left(a^{2}\right)}{k}, \quad \text { for all } a \in S .
$$
It follows that $f(a)=k$ for all $a \in S$. Substituting $a=2$ and $b=3$ into the functional equation yields $k=1$, however $1 \notin S$ and hence we have no solutions.
|
{
"problem_match": "\nProblem 2.",
"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl",
"solution_match": "\nSolution."
}
| 92
| 546
|
2015
|
T1
|
3
| null |
APMO
|
A sequence of real numbers $a_{0}, a_{1}, \ldots$ is said to be good if the following three conditions hold.
(i) The value of $a_{0}$ is a positive integer.
(ii) For each non-negative integer $i$ we have $a_{i+1}=2 a_{i}+1$ or $a_{i+1}=\frac{a_{i}}{a_{i}+2}$.
(iii) There exists a positive integer $k$ such that $a_{k}=2014$.
Find the smallest positive integer $n$ such that there exists a good sequence $a_{0}, a_{1}, \ldots$ of real numbers with the property that $a_{n}=2014$.
Answer: 60.
|
Note that
$$
a_{i+1}+1=2\left(a_{i}+1\right) \text { or } a_{i+1}+1=\frac{a_{i}+a_{i}+2}{a_{i}+2}=\frac{2\left(a_{i}+1\right)}{a_{i}+2} .
$$
Hence
$$
\frac{1}{a_{i+1}+1}=\frac{1}{2} \cdot \frac{1}{a_{i}+1} \text { or } \frac{1}{a_{i+1}+1}=\frac{a_{i}+2}{2\left(a_{i}+1\right)}=\frac{1}{2} \cdot \frac{1}{a_{i}+1}+\frac{1}{2} .
$$
Therefore,
$$
\frac{1}{a_{k}+1}=\frac{1}{2^{k}} \cdot \frac{1}{a_{0}+1}+\sum_{i=1}^{k} \frac{\varepsilon_{i}}{2^{k-i+1}}
$$
where $\varepsilon_{i}=0$ or 1 . Multiplying both sides by $2^{k}\left(a_{k}+1\right)$ and putting $a_{k}=2014$, we get
$$
2^{k}=\frac{2015}{a_{0}+1}+2015 \cdot\left(\sum_{i=1}^{k} \varepsilon_{i} \cdot 2^{i-1}\right)
$$
where $\varepsilon_{i}=0$ or 1 . Since $\operatorname{gcd}(2,2015)=1$, we have $a_{0}+1=2015$ and $a_{0}=2014$. Therefore,
$$
2^{k}-1=2015 \cdot\left(\sum_{i=1}^{k} \varepsilon_{i} \cdot 2^{i-1}\right)
$$
where $\varepsilon_{i}=0$ or 1 . We now need to find the smallest $k$ such that $2015 \mid 2^{k}-1$. Since $2015=$ $5 \cdot 13 \cdot 31$, from the Fermat little theorem we obtain $5\left|2^{4}-1,13\right| 2^{12}-1$ and $31 \mid 2^{30}-1$. We also have $\operatorname{lcm}[4,12,30]=60$, hence $5\left|2^{60}-1,13\right| 2^{60}-1$ and $31 \mid 2^{60}-1$, which gives $2015 \mid 2^{60}-1$.
But $5 \nmid 2^{30}-1$ and so $k=60$ is the smallest positive integer such that $2015 \mid 2^{k}-1$. To conclude, the smallest positive integer $k$ such that $a_{k}=2014$ is when $k=60$.
Alternative solution 1. Clearly all members of the sequence are positive rational numbers. For each positive integer $i$, we have $a_{i}=\frac{a_{i+1}-1}{2}$ or $a_{i}=\frac{2 a_{i+1}}{1-a_{i+1}}$. Since $a_{i}>0$ we deduce that
$$
a_{i}=\left\{\begin{array}{cl}
\frac{a_{i+1}-1}{2} & \text { if } a_{i+1}>1 \\
\frac{2 a_{i+1}}{1-a_{i+1}} & \text { if } a_{i+1}<1
\end{array}\right.
$$
Thus $a_{i}$ is uniquely determined from $a_{i+1}$. Hence starting from $a_{k}=2014$, we simply run the sequence backwards until we reach a positive integer. We compute as follows.
$$
\begin{aligned}
& \frac{2014}{1}, \frac{2013}{2}, \frac{2011}{4}, \frac{2007}{8}, \frac{1999}{16}, \frac{1983}{32}, \frac{1951}{64}, \frac{1887}{128}, \frac{1759}{256}, \frac{1503}{512}, \frac{991}{1024}, \frac{1982}{33}, \frac{1949}{66}, \frac{1883}{132}, \frac{1751}{264}, \frac{1487}{528}, \frac{959}{1056}, \frac{1918}{97}, \frac{1821}{194}, \frac{1627}{388}, \\
& \frac{1239}{776}, \frac{463}{1552}, \frac{926}{1089}, \frac{1852}{163}, \frac{1689}{326}, \frac{1363}{652}, \frac{711}{1304}, \frac{1422}{593}, \frac{829}{1186}, \frac{1658}{357}, \frac{1301}{714}, \frac{587}{1428}, \frac{1174}{841}, \frac{333}{1682}, \frac{666}{1349}, \frac{1332}{683}, \frac{649}{1366}, \frac{1298}{717}, \frac{581}{1434}, \frac{1162}{853}, \\
& \frac{309}{1706}, \frac{618}{1397}, \frac{1236}{779}, \frac{457}{1558}, \frac{914}{1101}, \frac{1828}{187}, \frac{1641}{374}, \frac{1267}{748}, \frac{519}{1496}, \frac{1038}{977}, \frac{61}{1954}, \frac{122}{1893}, \frac{244}{1771}, \frac{488}{1527}, \frac{976}{1039}, \frac{1952}{63}, \frac{1889}{126}, \frac{1763}{252}, \frac{1511}{504}, \frac{1007}{1008}, \frac{2014}{1}
\end{aligned}
$$
There are 61 terms in the above list. Thus $k=60$.
Alternative solution 1 is quite computationally intensive. Calculating the first few terms indicates some patterns that are easy to prove. This is shown in the next solution.
Alternative solution 2. Start with $a_{k}=\frac{m_{0}}{n_{0}}$ where $m_{0}=2014$ and $n_{0}=1$ as in alternative solution 1. By inverting the sequence as in alternative solution 1, we have $a_{k-i}=\frac{m_{i}}{n_{i}}$ for $i \geq 0$ where
$$
\left(m_{i+1}, n_{i+1}\right)= \begin{cases}\left(m_{i}-n_{i}, 2 n_{i}\right) & \text { if } m_{i}>n_{i} \\ \left(2 m_{i}, n_{i}-m_{i}\right) & \text { if } m_{i}<n_{i}\end{cases}
$$
Easy inductions show that $m_{i}+n_{i}=2015,1 \leq m_{i}, n_{i} \leq 2014$ and $\operatorname{gcd}\left(m_{i}, n_{i}\right)=1$ for $i \geq 0$. Since $a_{0} \in \mathbb{N}^{+}$and $\operatorname{gcd}\left(m_{k}, n_{k}\right)=1$, we require $n_{k}=1$. An easy induction shows that $\left(m_{i}, n_{i}\right) \equiv\left(-2^{i}, 2^{i}\right)(\bmod 2015)$ for $i=0,1, \ldots, k$.
Thus $2^{k} \equiv 1(\bmod 2015)$. As in the official solution, the smallest such $k$ is $k=60$. This yields $n_{k} \equiv 1(\bmod 2015)$. But since $1 \leq n_{k}, m_{k} \leq 2014$, it follows that $a_{0}$ is an integer.
|
{
"problem_match": "\nProblem 3.",
"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl",
"solution_match": "\nSolution."
}
| 172
| 2,195
|
2015
|
T1
|
4
| null |
APMO
|
Let $n$ be a positive integer. Consider $2 n$ distinct lines on the plane, no two of which are parallel. Of the $2 n$ lines, $n$ are colored blue, the other $n$ are colored red. Let $\mathcal{B}$ be the set of all points on the plane that lie on at least one blue line, and $\mathcal{R}$ the set of all points on the plane that lie on at least one red line. Prove that there exists a circle that intersects $\mathcal{B}$ in exactly $2 n-1$ points, and also intersects $\mathcal{R}$ in exactly $2 n-1$ points.
|
Consider a line $\ell$ on the plane and a point $P$ on it such that $\ell$ is not parallel to any of the $2 n$ lines. Rotate $\ell$ about $P$ counterclockwise until it is parallel to one of the $2 n$ lines. Take note of that line and keep rotating until all the $2 n$ lines are met. The $2 n$ lines are now ordered according to which line is met before or after. Say the lines are in order $\ell_{1}, \ldots, \ell_{2 n}$. Clearly there must be $k \in\{1, \ldots, 2 n-1\}$ such that $\ell_{k}$ and $\ell_{k+1}$ are of different colors.
Now we set up a system of $X-$ and $Y$ - axes on the plane. Consider the two angular bisectors of $\ell_{k}$ and $\ell_{k+1}$. If we rotate $\ell_{k+1}$ counterclockwise, the line will be parallel to one of the bisectors before the other. Let the bisector that is parallel to the rotation of $\ell_{k+1}$ first be the $X$-axis, and the other the $Y$-axis. From now on, we will be using the directed angle notation: for lines $s$ and $s^{\prime}$, we define $\angle\left(s, s^{\prime}\right)$ to be a real number in $[0, \pi)$ denoting the angle in radians such that when $s$ is rotated counterclockwise by $\angle\left(s, s^{\prime}\right)$ radian, it becomes parallel to $s^{\prime}$. Using this
notation, we notice that there is no $i=1, \ldots, 2 n$ such that $\angle\left(X, l_{i}\right)$ is between $\angle\left(X, \ell_{k}\right)$ and $\angle\left(X, \ell_{k+1}\right)$.
Because the $2 n$ lines are distinct, the set $S$ of all the intersections between $\ell_{i}$ and $\ell_{j}(i \neq j)$ is a finite set of points. Consider a rectangle with two opposite vertices lying on $\ell_{k}$ and the other two lying on $\ell_{k+1}$. With respect to the origin (the intersection of $\ell_{k}$ and $\ell_{k+1}$ ), we can enlarge the rectangle as much as we want, while all the vertices remain on the lines. Thus, there is one of these rectangles $R$ which contains all the points in $S$ in its interior. Since each side of $R$ is parallel to either $X$ - or $Y$ - axis, $R$ is a part of the four lines $x= \pm a, y= \pm b$. where $a, b>0$.
Consider the circle $\mathcal{C}$ tangent to the right of the $x=a$ side of the rectangle, and to both $\ell_{k}$ and $\ell_{k+1}$. We claim that this circle intersects $\mathcal{B}$ in exactly $2 n-1$ points, and also intersects $\mathcal{R}$ in exactly $2 n-1$ points. Since $\mathcal{C}$ is tangent to both $\ell_{k}$ and $\ell_{k+1}$ and the two lines have different colors, it is enough to show that $\mathcal{C}$ intersects with each of the other $2 n-2$ lines in exactly 2 points. Note that no two lines intersect on the circle because all the intersections between lines are in $S$ which is in the interior of $R$.
Consider any line $L$ among these $2 n-2$ lines. Let $L$ intersect with $\ell_{k}$ and $\ell_{k+1}$ at the points $M$ and $N$, respectively ( $M$ and $N$ are not necessarily distinct). Notice that both $M$ and $N$ must be inside $R$. There are two cases:
(i) $L$ intersects $R$ on the $x=-a$ side once and another time on $x=a$ side;
(ii) $L$ intersects $y=-b$ and $y=b$ sides.
However, if (ii) happens, $\angle\left(\ell_{k}, L\right)$ and $\angle\left(L, \ell_{k+1}\right)$ would be both positive, and then $\angle(X, L)$ would be between $\angle\left(X, \ell_{k}\right)$ and $\angle\left(X, \ell_{k+1}\right)$, a contradiction. Thus, only (i) can happen. Then $L$ intersects $\mathcal{C}$ in exactly two points, and we are done.
Alternative solution. By rotating the diagram we can ensure that no line is vertical. Let $\ell_{1}, \ell_{2}, \ldots, \ell_{2 n}$ be the lines listed in order of increasing gradient. Then there is a $k$ such that lines $\ell_{k}$ and $\ell_{k+1}$ are oppositely coloured. By rotating our coordinate system and cyclicly relabelling our lines we can ensure that $\ell_{1}, \ell_{2}, \ldots, \ell_{2 n}$ are listed in order of increasing gradient, $\ell_{1}$ and $\ell_{2 n}$ are oppositely coloured, and no line is vertical.
Let $\mathcal{D}$ be a circle centred at the origin and of sufficiently large radius so that
- All intersection points of all pairs of lines lie strictly inside $\mathcal{D}$; and
- Each line $\ell_{i}$ intersects $\mathcal{D}$ in two points $A_{i}$ and $B_{i}$ say, such that $A_{i}$ is on the right semicircle (the part of the circle in the positive $x$ half plane) and $B_{i}$ is on the left semicircle.
Note that the anticlockwise order of the points $A_{i}, B_{i}$ around $\mathcal{D}$ is $A_{1}, A_{2}, \ldots, A_{n}, B_{1}, B_{2}, \ldots, B_{n}$.
(If $A_{i+1}$ occurred before $A_{i}$ then rays $r_{i}$ and $r_{i+1}$ (as defined below) would intersect outside $\mathcal{D}$.)
For each $i$, let $r_{i}$ be the ray that is the part of the line $\ell_{i}$ starting from point $A_{i}$ and that extends to the right. Let $\mathcal{C}$ be any circle tangent to $r_{1}$ and $r_{2 n}$, that lies entirely to the right of $\mathcal{D}$. Then $\mathcal{C}$ intersects each of $r_{2}, r_{3}, \ldots, r_{2 n-1}$ twice and is tangent to $r_{1}$ and $r_{2 n}$. Thus $\mathcal{C}$ has the required properties.
|
{
"problem_match": "\nProblem 4.",
"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl",
"solution_match": "\nSolution."
}
| 144
| 1,562
|
2015
|
T1
|
5
| null |
APMO
|
Determine all sequences $a_{0}, a_{1}, a_{2}, \ldots$ of positive integers with $a_{0} \geq 2015$ such that for all integers $n \geq 1$ :
(i) $a_{n+2}$ is divisible by $a_{n}$;
(ii) $\left|s_{n+1}-(n+1) a_{n}\right|=1$, where $s_{n+1}=a_{n+1}-a_{n}+a_{n-1}-\cdots+(-1)^{n+1} a_{0}$.
Answer: There are two families of answers:
(a) $a_{n}=c(n+2) n$ ! for all $n \geq 1$ and $a_{0}=c+1$ for some integer $c \geq 2014$, and
(b) $a_{n}=c(n+2) n$ ! for all $n \geq 1$ and $a_{0}=c-1$ for some integer $c \geq 2016$.
|
Let $\left\{a_{n}\right\}_{n=0}^{\infty}$ be a sequence of positive integers satisfying the given conditions. We can rewrite (ii) as $s_{n+1}=(n+1) a_{n}+h_{n}$, where $h_{n} \in\{-1,1\}$. Substituting $n$ with $n-1$ yields $s_{n}=n a_{n-1}+h_{n-1}$, where $h_{n-1} \in\{-1,1\}$. Note that $a_{n+1}=s_{n+1}+s_{n}$, therefore there exists $\delta_{n} \in\{-2,0,2\}$ such that
$$
a_{n+1}=(n+1) a_{n}+n a_{n-1}+\delta_{n}
$$
We also have $\left|s_{2}-2 a_{1}\right|=1$, which yields $a_{0}=3 a_{1}-a_{2} \pm 1 \leq 3 a_{1}$, and therefore $a_{1} \geq \frac{a_{0}}{3} \geq 671$. Substituting $n=2$ in (1), we find that $a_{3}=3 a_{2}+2 a_{1}+\delta_{2}$. Since $a_{1} \mid a_{3}$, we have $a_{1} \mid 3 a_{2}+\delta_{2}$, and therefore $a_{2} \geq 223$. Using (1), we obtain that $a_{n} \geq 223$ for all $n \geq 0$.
Lemma 1: For $n \geq 4$, we have $a_{n+2}=(n+1)(n+4) a_{n}$.
Proof. For $n \geq 3$ we have
$$
a_{n}=n a_{n-1}+(n-1) a_{n-2}+\delta_{n-1}>n a_{n-1}+3 .
$$
By applying (2) with $n$ substituted by $n-1$ we have for $n \geq 4$,
$$
a_{n}=n a_{n-1}+(n-1) a_{n-2}+\delta_{n-1}<n a_{n-1}+\left(a_{n-1}-3\right)+\delta_{n-1}<(n+1) a_{n-1}
$$
Using (1) to write $a_{n+2}$ in terms of $a_{n}$ and $a_{n-1}$ along with (2), we obtain that for $n \geq 3$,
$$
\begin{aligned}
a_{n+2} & =(n+3)(n+1) a_{n}+(n+2) n a_{n-1}+(n+2) \delta_{n}+\delta_{n+1} \\
& <(n+3)(n+1) a_{n}+(n+2) n a_{n-1}+3(n+2) \\
& <\left(n^{2}+5 n+5\right) a_{n} .
\end{aligned}
$$
Also for $n \geq 4$,
$$
\begin{aligned}
a_{n+2} & =(n+3)(n+1) a_{n}+(n+2) n a_{n-1}+(n+2) \delta_{n}+\delta_{n+1} \\
& >(n+3)(n+1) a_{n}+n a_{n} \\
& =\left(n^{2}+5 n+3\right) a_{n} .
\end{aligned}
$$
Since $a_{n} \mid a_{n+2}$, we obtain that $a_{n+2}=\left(n^{2}+5 n+4\right) a_{n}=(n+1)(n+4) a_{n}$, as desired.
Lemma 2: For $n \geq 4$, we have $a_{n+1}=\frac{(n+1)(n+3)}{n+2} a_{n}$.
Proof. Using the recurrence $a_{n+3}=(n+3) a_{n+2}+(n+2) a_{n+1}+\delta_{n+2}$ and writing $a_{n+3}$, $a_{n+2}$ in terms of $a_{n+1}, a_{n}$ according to Lemma 1 we obtain
$$
(n+2)(n+4) a_{n+1}=(n+3)(n+1)(n+4) a_{n}+\delta_{n+2} .
$$
Hence $n+4 \mid \delta_{n+2}$, which yields $\delta_{n+2}=0$ and $a_{n+1}=\frac{(n+1)(n+3)}{n+2} a_{n}$, as desired.
Suppose there exists $n \geq 1$ such that $a_{n+1} \neq \frac{(n+1)(n+3)}{n+2} a_{n}$. By Lemma 2, there exist a greatest integer $1 \leq m \leq 3$ with this property. Then $a_{m+2}=\frac{(m+2)(m+4)}{m+3} a_{m+1}$. If $\delta_{m+1}=0$, we have $a_{m+1}=\frac{(m+1)(m+3)}{m+2} a_{m}$, which contradicts our choice of $m$. Thus $\delta_{m+1} \neq 0$.
Clearly $m+3 \mid a_{m+1}$. Write $a_{m+1}=(m+3) k$ and $a_{m+2}=(m+2)(m+4) k$. Then $(m+$ 1) $a_{m}+\delta_{m+1}=a_{m+2}-(m+2) a_{m+1}=(m+2) k$. So, $a_{m} \mid(m+2) k-\delta_{m+1}$. But $a_{m}$ also divides $a_{m+2}=(m+2)(m+4) k$. Combining the two divisibility conditions, we obtain $a_{m} \mid(m+4) \delta_{m+1}$. Since $\delta_{m+1} \neq 0$, we have $a_{m} \mid 2 m+8 \leq 14$, which contradicts the previous result that $a_{n} \geq 223$ for all nonnegative integers $n$.
So, $a_{n+1}=\frac{(n+1)(n+3)}{n+2} a_{n}$ for $n \geq 1$. Substituting $n=1$ yields $3 \mid a_{1}$. Letting $a_{1}=3 c$, we have by induction that $a_{n}=n!(n+2) c$ for $n \geq 1$. Since $\left|s_{2}-2 a_{1}\right|=1$, we then get $a_{0}=c \pm 1$, yielding the two families of solutions. By noting that $(n+2) n!=n!+(n+1)!$, we have $s_{n+1}=c(n+2)!+(-1)^{n}\left(c-a_{0}\right)$. Hence both families of solutions satisfy the given conditions.
|
{
"problem_match": "\nProblem 5.",
"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl",
"solution_match": "\nSolution."
}
| 246
| 1,743
|
2016
|
T1
|
1
| null |
APMO
|
We say that a triangle $A B C$ is great if the following holds: for any point $D$ on the side $B C$, if $P$ and $Q$ are the feet of the perpendiculars from $D$ to the lines $A B$ and $A C$, respectively, then the reflection of $D$ in the line $P Q$ lies on the circumcircle of the triangle $A B C$.
Prove that triangle $A B C$ is great if and only if $\angle A=90^{\circ}$ and $A B=A C$.
|
For every point $D$ on the side $B C$, let $D^{\prime}$ be the reflection of $D$ in the line $P Q$. We will first prove that if the triangle satisfies the condition then it is isosceles and right-angled at $A$.
Choose $D$ to be the point where the angle bisector from $A$ meets $B C$. Note that $P$ and $Q$ lie on the rays $A B$ and $A C$ respectively. Furthermore, $P$ and $Q$ are reflections of each other in the line $A D$, from which it follows that $P Q \perp A D$. Therefore, $D^{\prime}$ lies on the line $A D$ and we may deduce that either $D^{\prime}=A$ or $D^{\prime}$ is the second point of the angle bisector at $A$ and the circumcircle of $A B C$. However, since $A P D Q$ is a cyclic quadrilateral, the segment $P Q$ intersects the segment $A D$. Therefore, $D^{\prime}$ lies on the ray $D A$ and therefore $D^{\prime}=A$. By angle chasing we obtain
$$
\angle P D^{\prime} Q=\angle P D Q=180^{\circ}-\angle B A C
$$
and since $D^{\prime}=A$ we also know $\angle P D^{\prime} Q=\angle B A C$. This implies that $\angle B A C=90^{\circ}$.
Now we choose $D$ to be the midpoint of $B C$. Since $\angle B A C=90^{\circ}$, we can deduce that $D Q P$ is the medial triangle of triangle $A B C$. Therefore, $P Q \| B C$ from which it follows that $D D^{\prime} \perp B C$. But the distance from $D^{\prime}$ to $B C$ is equal to both the circumradius of triangle $A B C$ and to the distance from $A$ to $B C$. This can only happen if $A=D^{\prime}$. This implies that $A B C$ is isosceles and right-angled at $A$.
We will now prove that if $A B C$ is isosceles and right-angled at $A$ then the required property in the problem holds. Let $D$ be any point on side $B C$. Then $D^{\prime} P=D P$ and we also have $D P=B P$. Hence, $D^{\prime} P=B P$ and similarly $D^{\prime} Q=C Q$. Note that $A P D Q D^{\prime}$ is cyclic with diameter $P Q$. Therefore, $\angle A P D^{\prime}=\angle A Q D^{\prime}$, from which we obtain $\angle B P D^{\prime}=\angle C Q D^{\prime}$. So triangles $D^{\prime} P B$ and $D^{\prime} Q C$ are similar. It follows that $\angle P D^{\prime} Q=\angle P D^{\prime} C+\angle C D^{\prime} Q=$ $\angle P D^{\prime} C+\angle B D^{\prime} P=\angle B D^{\prime} C$ and $\frac{D^{\prime} P}{D^{\prime} Q}=\frac{D^{\prime} B}{D^{\prime} C}$. So we also obtain that triangles $D^{\prime} P Q$ and $D^{\prime} B C$ are similar. But since $D P Q$ and $D^{\prime} P Q$ are congruent, we may deduce that $\angle B D^{\prime} C=$ $\angle P D^{\prime} Q=\angle P D Q=90^{\circ}$. Therefore, $D^{\prime}$ lies on the circle with diameter $B C$, which is the circumcircle of triangle $A B C$.
|
{
"problem_match": "\nProblem 1.",
"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl",
"solution_match": "\nSolution."
}
| 123
| 883
|
2016
|
T1
|
2
| null |
APMO
|
A positive integer is called fancy if it can be expressed in the form
$$
2^{a_{1}}+2^{a_{2}}+\cdots+2^{a_{100}}
$$
where $a_{1}, a_{2}, \ldots, a_{100}$ are non-negative integers that are not necessarily distinct.
Find the smallest positive integer $n$ such that no multiple of $n$ is a fancy number.
Answer: The answer is $n=2^{101}-1$.
|
Let $k$ be any positive integer less than $2^{101}-1$. Then $k$ can be expressed in binary notation using at most 100 ones, and therefore there exists a positive integer $r$ and non-negative integers $a_{1}, a_{2}, \ldots, a_{r}$ such that $r \leq 100$ and $k=2^{a_{1}}+\cdots+2^{a_{r}}$. Notice that for a positive integer $s$ we have:
$$
\begin{aligned}
2^{s} k & =2^{a_{1}+s}+2^{a_{2}+s}+\cdots+2^{a_{r-1}+s}+\left(1+1+2+\cdots+2^{s-1}\right) 2^{a_{r}} \\
& =2^{a_{1}+s}+2^{a_{2}+s}+\cdots+2^{a_{r-1}+s}+2^{a_{r}}+2^{a_{r}}+\cdots+2^{a_{r}+s-1} .
\end{aligned}
$$
This shows that $k$ has a multiple that is a sum of $r+s$ powers of two. In particular, we may take $s=100-r \geq 0$, which shows that $k$ has a multiple that is a fancy number.
We will now prove that no multiple of $n=2^{101}-1$ is a fancy number. In fact we will prove a stronger statement, namely, that no multiple of $n$ can be expressed as the sum of at most 100 powers of 2 .
For the sake of contradiction, suppose that there exists a positive integer $c$ such that $c n$ is the sum of at most 100 powers of 2 . We may assume that $c$ is the smallest such integer. By repeatedly merging equal powers of two in the representation of $c n$ we may assume that
$$
c n=2^{a_{1}}+2^{a_{2}}+\cdots+2^{a_{r}}
$$
where $r \leq 100$ and $a_{1}<a_{2}<\ldots<a_{r}$ are distinct non-negative integers. Consider the following two cases:
- If $a_{r} \geq 101$, then $2^{a_{r}}-2^{a_{r}-101}=2^{a_{r}-101} n$. It follows that $2^{a_{1}}+2^{a_{2}}+\cdots+2^{a_{r}-1}+2^{a_{r}-101}$ would be a multiple of $n$ that is smaller than $c n$. This contradicts the minimality of $c$.
- If $a_{r} \leq 100$, then $\left\{a_{1}, \ldots, a_{r}\right\}$ is a proper subset of $\{0,1, \ldots, 100\}$. Then
$$
n \leq c n<2^{0}+2^{1}+\cdots+2^{100}=n
$$
This is also a contradiction.
From these contradictions we conclude that it is impossible for cn to be the sum of at most 100 powers of 2 . In particular, no multiple of $n$ is a fancy number.
|
{
"problem_match": "\nProblem 2.",
"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl",
"solution_match": "\nSolution."
}
| 111
| 770
|
2016
|
T1
|
3
| null |
APMO
|
Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\omega$.
|
.
Let the line through $N$ tangent to $\omega$ at point $X \neq E$ intersect $A B$ at point $M^{\prime}$. It suffices to show that $M^{\prime} R \| A C$, since this would yield $M^{\prime}=M$.
Suppose that the line $P O$ intersects $A C$ at $Q$ and the circumcircle of $A M^{\prime} O$ at $Y$, respectively. Then
$$
\angle A Y M^{\prime}=\angle A O M^{\prime}=90^{\circ}-\angle M^{\prime} O P
$$
By angle chasing we have $\angle E O Q=\angle F O P=90^{\circ}-\angle A O F=\angle M^{\prime} A O=\angle M^{\prime} Y P$ and by symmetry $\angle E Q O=\angle M^{\prime} P Y$. Therefore $\triangle M^{\prime} Y P \sim \triangle E O Q$.
On the other hand, we have
$$
\begin{aligned}
\angle M^{\prime} O P & =\angle M^{\prime} O F+\angle F O P=\frac{1}{2}(\angle F O X+\angle F O P+\angle E O Q)= \\
& =\frac{1}{2}\left(\frac{180^{\circ}-\angle X O E}{2}\right)=90^{\circ}-\frac{\angle X O E}{2} .
\end{aligned}
$$
Since we know that $\angle A Y M^{\prime}$ and $\angle M^{\prime} O P$ are complementary this implies
$$
\angle A Y M^{\prime}=\frac{\angle X O E}{2}=\angle N O E
$$
Therefore, $\angle A Y M^{\prime}$ and $\angle N O E$ are congruent angles, and this means that $A$ and $N$ are corresponding points in the similarity of triangles $\triangle M^{\prime} Y P$ and $\triangle E O Q$. It follows that
$$
\frac{A M^{\prime}}{M^{\prime} P}=\frac{N E}{E Q}=\frac{N R}{R P}
$$
We conclude that $M^{\prime} R \| A C$, as desired.
|
{
"problem_match": "\nProblem 3.",
"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl",
"solution_match": "# Solution 1"
}
| 151
| 522
|
2016
|
T1
|
3
| null |
APMO
|
Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\omega$.
|
a.
As in Solution 1, we introduce point $M^{\prime}$ and reduce the problem to proving $\frac{P R}{R N}=\frac{P M^{\prime}}{M^{\prime} A}$. Menelaus theorem in triangle $A N P$ with transversal line $F R E$ yields
$$
\frac{P R}{R N} \cdot \frac{N E}{E A} \cdot \frac{A F}{F P}=1
$$
Since $A F=E A$, we have $\frac{F P}{N E}=\frac{P R}{R N}$, so that it suffices to prove
$$
\frac{F P}{N E}=\frac{P M^{\prime}}{M^{\prime} A}
$$
This is a computation regarding the triangle $A M^{\prime} N$ and its excircle opposite $A$. Indeed, setting $a=M^{\prime} N, b=N A, c=M^{\prime} A, s=\frac{a+b+c}{2}, x=s-a, y=s-b$ and $z=s-c$, then $A E=A F=s, M^{\prime} F=z$ and $N E=y$. From $\triangle O F P \sim \triangle A F O$ we have $F P=\frac{r_{a}^{2}}{s}$, where $r_{a}=O F$ is the exradius opposite $A$. Combining the following two standard formulas for the area of a triangle
$$
\left|A M^{\prime} N\right|^{2}=x y z s \quad \text { (Heron's formula) and } \quad\left|A M^{\prime} N\right|=r_{a}(s-a),
$$
we have $r_{a}^{2}=\frac{y z s}{x}$. Therefore, $F P=\frac{y z}{x}$. We can now write everything in (1) in terms of $x, y, z$. We conclude that we have to verify
$$
\frac{\frac{y z}{x}}{y}=\frac{z+\frac{y z}{x}}{x+y}
$$
which is easily seen to be true.
Note: Antoher approach using Menalaus theorem is to construct the tangent from $M$ to create a point $N^{\prime}$ in $A C$ and then prove, using the theorem, that $P, R$ and $N^{\prime}$ are collinear. This also reduces to an algebraic identity.
|
{
"problem_match": "\nProblem 3.",
"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl",
"solution_match": "# Solution 2"
}
| 151
| 564
|
2016
|
T1
|
3
| null |
APMO
|
Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\omega$.
|
b.
As in Solution 1, we introduce point $M^{\prime}$. Let the line through $M^{\prime}$ and parallel to $A N$ intersect $E F$ at $R^{\prime}$. Let $P^{\prime}$ be the intersection of lines $N R^{\prime}$ and $A M$. It suffices to show that $P^{\prime} O \| F E$, since this would yield $P=P^{\prime}$, and then $R=R^{\prime}$ and $M=M^{\prime}$. Hence it is enough to prove that
$$
\frac{A F}{F P^{\prime}}=\frac{A D}{D O}
$$
where $D$ is the intersection of $A O$ and $E F$. Once again, this reduces to a computation regarding the triangle $A M^{\prime} N$ and its excircle opposite $A$.
Let $u=P^{\prime} F$ and $x, y, z, s$ as in Solution 2a. Note that since $A E=A F$ and $M^{\prime} R^{\prime} \| A E$, we have $M^{\prime} R^{\prime}=M^{\prime} F=z$. Since $M^{\prime} R^{\prime} \| A N$, we have $\frac{P^{\prime} M^{\prime}}{P^{\prime} A}=\frac{M^{\prime} R^{\prime}}{N A}$, that is,
$$
\frac{u+z}{u+x+y+z}=\frac{z}{x+z}
$$
From this last equation we obtain $u=\frac{y z}{x}$. Hence $\frac{A F}{F P^{\prime}}=\frac{x s}{y z}$. Also, as in Solution 2a, we have $r_{a}^{2}=\frac{y z s}{x}$.
Finally, using similar triangles $O D F, F D A$ and $O F A$, and the above equalities, we have
$$
\frac{A D}{D O}=\frac{A D}{D F} \cdot \frac{D F}{D O}=\frac{A F}{O F} \cdot \frac{A F}{O F}=\frac{s^{2}}{r_{a}^{2}}=\frac{s^{2}}{\frac{y z s}{x}}=\frac{x s}{y z}=\frac{A F}{F P^{\prime}}
$$
as required.
|
{
"problem_match": "\nProblem 3.",
"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl",
"solution_match": "# Solution 2"
}
| 151
| 556
|
2016
|
T1
|
5
| null |
APMO
|
Find all functions $f: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+}$such that
$$
(z+1) f(x+y)=f(x f(z)+y)+f(y f(z)+x)
$$
for all positive real numbers $x, y, z$.
Answer: The only solution is $f(x)=x$ for all positive real numbers $x$.
|
The identity function $f(x)=x$ clearly satisfies the functional equation. Now, let $f$ be a function satisfying the functional equation. Plugging $x=y=1$ into (3) we get $2 f(f(z)+1)=(z+1)(f(2))$ for all $z \in \mathbb{R}^{+}$. Hence, $f$ is not bounded above.
Lemma. Let $a, b, c$ be positive real numbers. If $c$ is greater than $1, a / b$ and $b / a$, then the system of linear equations
$$
c u+v=a \quad u+c v=b
$$
has a positive real solution $u, v$.
Proof. The solution is
$$
u=\frac{c a-b}{c^{2}-1} \quad v=\frac{c b-a}{c^{2}-1} .
$$
The numbers $u$ and $v$ are positive if the conditions on $c$ above are satisfied.
We will now prove that
$$
f(a)+f(b)=f(c)+f(d) \quad \text { for all } a, b, c, d \in \mathbb{R}^{+} \text {with } a+b=c+d
$$
Consider $a, b, c, d \in \mathbb{R}^{+}$such that $a+b=c+d$. Since $f$ is not bounded above, we can choose a positive number $e$ such that $f(e)$ is greater than $1, a / b, b / a, c / d$ and $d / c$. Using the above lemma, we can find $u, v, w, t \in \mathbb{R}^{+}$satisfying
$$
\begin{array}{ll}
f(e) u+v=a, & u+f(e) v=b \\
f(e) w+t=c, & w+f(e) t=d .
\end{array}
$$
Note that $u+v=w+t$ since $(u+v)(f(e)+1)=a+b$ and $(w+t)(f(e)+1)=c+d$. Plugging $x=u, y=v$ and $z=e$ into (3) yields $f(a)+f(b)=(e+1) f(u+v)$. Similarly, we have $f(c)+f(d)=(e+1) f(w+t)$. The claim follows immediately.
We then have
$$
y f(x)=f(x f(y)) \quad \text { for all } x, y \in \mathbb{R}^{+}
$$
since by (3) and (4),
$$
(y+1) f(x)=f\left(\frac{x}{2} f(y)+\frac{x}{2}\right)+f\left(\frac{x}{2} f(y)+\frac{x}{2}\right)=f(x f(y))+f(x) .
$$
Now, let $a=f(1 / f(1))$. Plugging $x=1$ and $y=1 / f(1)$ into (5) yields $f(a)=1$. Hence $a=a f(a)$ and $f(a f(a))=f(a)=1$. Since $a f(a)=f(a f(a))$ by (5), we have $f(1)=a=1$. It follows from (5) that
$$
f(f(y))=y \quad \text { for all } y \in \mathbb{R}^{+} .
$$
Using (4) we have for all $x, y \in \mathbb{R}^{+}$that
$$
\begin{aligned}
& f(x+y)+f(1)=f(x)+f(y+1), \quad \text { and } \\
& f(y+1)+f(1)=f(y)+f(2)
\end{aligned}
$$
Therefore
$$
f(x+y)=f(x)+f(y)+b \quad \text { for all } x, y \in \mathbb{R}^{+},
$$
where $b=f(2)-2 f(1)=f(2)-2$. Using (5), (7) and (6), we get
$$
4+2 b=2 f(2)=f(2 f(2))=f(f(2)+f(2))=f(f(2))+f(f(2))+b=4+b
$$
This shows that $b=0$ and thus
$$
f(x+y)=f(x)+f(y) \quad \text { for all } x, y \in \mathbb{R}^{+} .
$$
In particular, $f$ is strictly increasing.
We conclude as follows. Take any positive real number $x$. If $f(x)>x$, then $f(f(x))>$ $f(x)>x=f(f(x))$, a contradiction. Similarly, it is not possible that $f(x)<x$. This shows that $f(x)=x$ for all positive real numbers $x$.
|
{
"problem_match": "\nProblem 5.",
"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl",
"solution_match": "\nSolution."
}
| 88
| 1,085
|
2017
|
T1
|
2
| null |
APMO
|
Let $A B C$ be a triangle with $A B<A C$. Let $D$ be the intersection point of the internal bisector of angle $B A C$ and the circumcircle of $A B C$. Let $Z$ be the intersection point of the perpendicular bisector of $A C$ with the external bisector of angle $\angle B A C$. Prove that the midpoint of the segment $A B$ lies on the circumcircle of triangle $A D Z$.
|
. Let $N$ be the midpoint of $A C$. Let $M$ be the intersection point of the circumcircle of triangle $A D Z$ and the segment $A B$. We will show that $M$ is the midpoint of $A B$. To do this, let $D^{\prime}$ the reflection of $D$ with respect to $M$. It suffices to show that $A D B D^{\prime}$ is a parallelogram.
The internal and external bisectors of an angle in a triangle are perpendicular. This implies that $Z D$ is a diameter of the circumcircle of $A Z D$ and thus $\angle Z M D=90^{\circ}$. This means that $Z M$ is the perpendicular bisector of $D^{\prime} D$ and thus $Z D^{\prime}=Z D$. By construction, $Z$ is in the perpendicular bisector of $A C$ and thus $Z A=Z C$.
Now, let $\alpha$ be the angle $\angle B A D=\angle D A C$. In the cyclic quadrilateral $A Z D M$ we get $\angle M Z D=\angle M A D=\alpha$, and thus $\angle D^{\prime} Z D=2 \alpha$. By angle chasing we get
$$
\angle A Z N=90^{\circ}-\angle Z A N=\angle D A C=\alpha,
$$
which implies that $\angle A Z C=2 \alpha$. Therefore,
$$
\angle D^{\prime} Z A=\angle D^{\prime} Z D-\angle A Z D=2 \alpha-\angle A Z D=\angle A Z C-\angle A Z D=\angle D Z C .
$$
Combining $\angle D^{\prime} Z A=\angle D Z C, Z D^{\prime}=Z D$ and $Z A=Z C$, we obtain by the $S A S$ criterion that the triangles $D^{\prime} Z A$ and $D Z C$ are congruent. In particular, $D^{\prime} A=D C$ and $\angle D^{\prime} A Z=$ $\angle D C Z$. From here $D B=D C=D^{\prime} A$.
Finally, let $\beta=\angle A B C=\angle A D C$. We get the first of the following equalities by the sum of angles around point $A$ and the second one by the sum of internal angles of quadrilateral $A Z C D$
$$
\begin{aligned}
& 360^{\circ}=\angle D^{\prime} A Z+\angle Z A D+\angle D A B+\angle B A D^{\prime}=\angle D^{\prime} A Z+90^{\circ}+\alpha+\angle B A D^{\prime} \\
& 360^{\circ}=\angle D C Z+\angle Z A D+\angle C Z A+\angle A D C=\angle D C Z+90^{\circ}+2 \alpha+\beta
\end{aligned}
$$
By canceling equal terms we conclude that $\angle B A D^{\prime}=\alpha+\beta$. Also, $\angle A B D=\alpha+\beta$. Therefore, the segments $D^{\prime} A$ and $D B$ are parallel and have the same length. We conclude that $A D B D^{\prime}$ is a parallelogram. As the diagonals of a parallelogram intersect at their midpoints, we obtain that $M$ is the midpoint of $A B$ as desired.
Variant of solution. The solution above is indirect in the sense that it assumes that $M$ is in the circumcircle of $A Z D$ and then shows that $M$ is the midpoint of $A B$. We point out that the same ideas in the solution can be used to give a direct solution. Here we present a sketch on how to proceed in this manner.
Now we know that $M$ is the midpoint of the side $A B$. We construct the point $D^{\prime}$ in the same way. Now we have directly that $A D B D^{\prime}$ is a parallelogram and thus $D^{\prime} A=D B=D C$. By construction $Z A=Z C$. Also, the two sums of angles equal to $360^{\circ}$ in the previous solution let us conclude that $\angle D^{\prime} A Z=\angle D C Z$. Once again, we use (differently) the $S A S$ criterion and obtain that the triangles $D^{\prime} A Z$ and $D C Z$ are congruent. Thus, $D^{\prime} Z=D Z$.
We finish the problem by noting that $Z M$ is a median of the isosceles triangle $D^{\prime} Z D$, so it is also a perpendicular bisector. This shows that $\angle D M Z=90^{\circ}=\angle D A Z$, and therefore $M$ lies in the circumcircle of $D A Z$.
|
{
"problem_match": "\nProblem 2.",
"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl",
"solution_match": "\nSolution 1"
}
| 101
| 1,094
|
2017
|
T1
|
3
| null |
APMO
|
Let $A(n)$ denote the number of sequences $a_{1} \geq a_{2} \geq \ldots \geq a_{k}$ of positive integers for which $a_{1}+\cdots+a_{k}=n$ and each $a_{i}+1$ is a power of two $(i=1,2, \ldots, k)$. Let $B(n)$ denote the number of sequences $b_{1} \geq b_{2} \geq \ldots \geq b_{m}$ of positive integers for which $b_{1}+\cdots+b_{m}=n$ and each inequality $b_{j} \geq 2 b_{j+1}$ holds $(j=1,2, \ldots, m-1)$.
Prove that $A(n)=B(n)$ for every positive integer $n$.
|
We say that a sequence $a_{1} \geq a_{2} \geq \ldots \geq a_{k}$ of positive integers has type $A$ if $a_{i}+1$ is a power of two for $i=1,2, \ldots, k$. We say that a sequence $b_{1} \geq b_{2} \geq \ldots \geq b_{m}$ of positive integer has type $B$ if $b_{j} \geq 2 b_{j+1}$ for $j=1,2, \ldots, m-1$.
Recall that the binary representation of a positive integer expresses it as a sum of distinct powers of two in a unique way. Furthermore, we have the following formula for every positive integer $N$
$$
2^{N}-1=2^{N-1}+2^{N-2}+\cdots+2^{1}+2^{0}
$$
Given a sequence $a_{1} \geq a_{2} \geq \ldots \geq a_{k}$ of type $A$, use the preceding formula to express each term as a sum of powers of two. Write these powers of two in left-aligned rows, in decreasing order of size. By construction, $a_{i}$ is the sum of the numbers in the $i$ th row. For example, we obtain the following array when we start with the type A sequence $15,15,7,3,3,3,1$.
| 8 | 4 | 2 | 1 |
| :--- | :--- | :--- | :--- |
| 8 | 4 | 2 | 1 |
| 4 | 2 | 1 | |
| 2 | 1 | | |
| 2 | 1 | | |
| 2 | 1 | | |
| 1 | | | |
| 27 | 13 | 5 | 2 |
Define the sequence $b_{1}, b_{2}, \ldots, b_{n}$ by setting $b_{j}$ to be the sum of the numbers in the $j$ th column of the array. For example, we obtain the sequence $27,13,5,2$ from the array above. We now show that this new sequence has type B. This is clear from the fact that each column in the array contains at least as many entries as the column to the right of it and that each number larger than 1 in the array is twice the number to the right of it. Furthermore, it is clear that $a_{1}+a_{2}+\cdots+a_{k}=b_{1}+b_{2}+\cdots+b_{m}$, since both are equal to the sum of all the entries in the array.
We now show that we can do this operation backwards. Suppose that we are given a type B sequence $b_{1} \geq b_{2} \geq \ldots \geq b_{m}$. We construct an array inductively as follows:
- We fill $b_{m}$ left-aligned rows with the numbers $2^{m-1}, 2^{m-2}, \ldots, 2^{1}, 2^{0}$.
- Then we fill $b_{m-1}-2 b_{m}$ left aligned rows with the numbers $2^{m-2}, 2^{m-3}, \ldots, 2^{1}, 2^{0}$.
- Then we fill $b_{m-2}-2 b_{m-1}$ left aligned rows with the numbers $2^{m-3}, 2^{m-4}, \ldots, 2^{1}, 2^{0}$, and so on.
- In the last step we fill $b_{1}-2 b_{2}$ left-aligned rows with the number 1 .
For example, if we start with the type B sequence $27,13,5,2$, we obtain once again the array above. We define the sequence $a_{1}, a_{2}, \ldots, a_{k}$ by setting $a_{i}$ to be the sum of the numbers in the $i$ th row of the array. By construction, this sequence has type A. Furthermore, it is clear that $a_{1}+\cdots+a_{k}=b_{1}+\cdots+b_{m}$, since once again both sums are equal to the sum of all the entries in the array.
We have defined an operation that starts with a sequence of type A , produces an array whose row sums are given by the sequence, and outputs a sequence of type B corresponding to the column sums. We have also defined an operation that starts with a sequence of type B, produces an array whose column sums are given by the sequence, and outputs a sequence of type A corresponding to the row sums. The arrays produced in both cases comprise leftaligned rows of the form $2^{N-1}, 2^{N-2}, \ldots, 2^{1}, 2^{0}$, with non-increasing lengths. Let us refer to arrays obeying these properties as marvelous.
To show that these two operations are inverses of each other, it then suffices to prove that marvelous arrays are uniquely defined by either their row sums or their column sums. The former is obviously true and the latter arises from the observation that each step in the above inductive algorithm was forced in order to create a marvelous array with the prescribed column sums.
Thus, we have produced a bijection between the sequences of type A with sum $n$ and the sequences of type B with sum $n$. So we can conclude that $A(n)=B(n)$ for every positive integer $n$.
Remark The solution above provides a bijection between type A and type B sequences via an algorithm. There are alternative ways to provide such a bijection. For example, given the numbers $a_{1} \geq \ldots \geq a_{k}$ we may define the $b_{i}$ 's as
$$
b_{j}=\sum_{i}\left\lfloor\frac{a_{i}+1}{2^{j}}\right\rfloor .
$$
Conversely, given the numbers $b_{1} \geq \ldots \geq b_{m}$, one may define the $a_{i}$ 's by taking, as in the solution, $b_{m}$ numbers equal to $2^{m}-1, b_{m-1}-2 b_{m}$ numbers equal to $2^{m-1}-1, \ldots$, and $b_{1}-2 b_{2}$ numbers equal to $2^{1}-1$. One now needs to verify that these maps are mutually inverse.
|
{
"problem_match": "\nProblem 3.",
"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl",
"solution_match": "\nSolution."
}
| 190
| 1,464
|
2017
|
T1
|
4
| null |
APMO
|
Call a rational number $r$ powerful if $r$ can be expressed in the form $\frac{p^{k}}{q}$ for some relatively prime positive integers $p, q$ and some integer $k>1$. Let $a, b, c$ be positive
rational numbers such that $a b c=1$. Suppose there exist positive integers $x, y, z$ such that $a^{x}+b^{y}+c^{z}$ is an integer. Prove that $a, b, c$ are all powerful.
|
Let $a=\frac{a_{1}}{b_{1}}, b=\frac{a_{2}}{b_{2}}$, where $\operatorname{gcd}\left(a_{1}, b_{1}\right)=\operatorname{gcd}\left(a_{2}, b_{2}\right)=1$. Then $c=\frac{b_{1} b_{2}}{a_{1} a_{2}}$. The condition that $a^{x}+b^{y}+c^{z}$ is an integer becomes
$$
\frac{a_{1}^{x+z} a_{2}^{z} b_{2}^{y}+a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z}}{a_{1}^{z} a_{2}^{z} b_{1}^{x} b_{2}^{y}} \in \mathbb{Z}
$$
which can be restated as
$$
a_{1}^{z} a_{2}^{z} b_{1}^{x} b_{2}^{y} \mid a_{1}^{x+z} a_{2}^{z} b_{2}^{y}+a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z} .
$$
In particular, $a_{1}^{z}$ divides the right-hand side. Since it divides the first and second terms in the sum, we conclude that $a_{1}^{z} \mid b_{1}^{x+z} b_{2}^{y+z}$. Since $\operatorname{gcd}\left(a_{1}, b_{1}\right)=1$, we have $a_{1}^{z} \mid b_{2}^{y+z}$.
Let $p$ be a prime that divides $a_{1}$. Let $m, n \geq 1$ be integers such that $p^{n} \| a_{1}$ (i.e. $p^{n} \mid a_{1}$ but $\left.p^{n+1} \nmid a_{1}\right)$ and $p^{m} \| b_{2}$. The fact that $a_{1}^{z} \mid b_{2}^{y+z}$ implies $n z \leq m(y+z)$. Since $\operatorname{gcd}\left(a_{1}, b_{1}\right)=$ $\operatorname{gcd}\left(a_{2}, b_{2}\right)=1$, we have $p$ does not divide $b_{1}$ and does not divide $a_{2}$. Thus
$$
p^{n z} \| a_{1}^{z} a_{2}^{y+z} b_{1}^{x} \text { and } p^{m(y+z)} \| b_{1}^{x+z} b_{2}^{y+z}
$$
On the other hand, (1) implies that
$$
p^{n z+m y} \mid a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z} .
$$
If $n z<m(y+z)$, then (2) gives $p^{n z} \| a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z}$, which contradicts (3). Thus $n z=m(y+z)$ so $n$ is divisible by $k:=\frac{y+z}{\operatorname{gcd}(z, y+z)}>1$. Thus each exponent in the prime decomposition of $a_{1}$ must be divisible by $k$. Hence $a_{1}$ is a perfect $k$-power which means $a$ is powerful. Similarly, $b$ and $c$ are also powerful.
|
{
"problem_match": "\nProblem 4.",
"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl",
"solution_match": "\nSolution."
}
| 117
| 887
|
2017
|
T1
|
5
| null |
APMO
|
Let $n$ be a positive integer. A pair of $n$-tuples $\left(a_{1}, \ldots, a_{n}\right)$ and $\left(b_{1}, \ldots, b_{n}\right)$ with integer entries is called an exquisite pair if
$$
\left|a_{1} b_{1}+\cdots+a_{n} b_{n}\right| \leq 1
$$
Determine the maximum number of distinct $n$-tuples with integer entries such that any two of them form an exquisite pair.
Answer: The maximum is $n^{2}+n+1$.
|
First, we construct an example with $n^{2}+n+1 n$-tuples, each two of them forming an exquisite pair. In the following list, $*$ represents any number of zeros as long as the total number of entries is $n$.
- (*)
- $(*, 1, *)$
- $(*,-1, *)$
- $(*, 1, *, 1, *)$
- $(*, 1, *,-1, *)$
For example, for $n=2$ we have the tuples $(0,0),(0,1),(1,0),(0,-1),(-1,0),(1,1),(1,-1)$. The total number of such tuples is $1+n+n+\binom{n}{2}+\binom{n}{2}=n^{2}+n+1$. For any two of them, at most two of the products $a_{i} b_{i}$ are non-zero. The only case in which two of them are non-zero is when we take a sequence $(*, 1, *, 1, *)$ and a sequence $(*, 1, *,-1, *)$ with zero entries in the same places. But in this case one $a_{i} b_{i}$ is 1 and the other -1 . This shows that any two of these sequences form an exquisite pair.
Next, we claim that among any $n^{2}+n+2$ tuples, some two of them do not form an exquisite pair. We begin with lemma.
Lemma. Given $2 n+1$ distinct non-zero $n$-tuples of real numbers, some two of them $\left(a_{1}, \ldots, a_{n}\right)$ and $\left(b_{1}, \ldots, b_{n}\right)$ satisfy $a_{1} b_{1}+\cdots+a_{n} b_{n}>0$.
Proof of Lemma. We proceed by induction. The statement is easy for $n=1$ since for every three non-zero numbers there are two of them with the same sign. Assume that the statement is true for $n-1$ and consider $2 n+1$ tuples with $n$ entries. Since we are working with tuples of real numbers, we claim that we may assume that one of the tuples is $a=(0,0, \ldots, 0,-1)$. Let us postpone the proof of this claim for the moment.
If one of the remaining tuples $b$ has a negative last entry, then $a$ and $b$ satisfy the desired condition. So we may assume all the remaining tuples has a non-negative last entry. Now, from each tuple remove the last number. If two $n$-tuples $b$ and $c$ yield the same $(n-1)$-tuple, then
$$
b_{1} c_{1}+\cdots+b_{n-1} c_{n-1}+b_{n} c_{n}=b_{1}^{2}+\cdots+b_{n-1}^{2}+b_{n} c_{n}>0
$$
and we are done. The remaining case is that all the $n$-tuples yield distinct ( $n-1$ )-tuples. Then at most one of them is the zero $(n-1)$-tuple, and thus we can use the inductive hypothesis on $2 n-1$ of them. So we find $b$ and $c$ for which
$$
\left(b_{1} c_{1}+\cdots+b_{n-1} c_{n-1}\right)+b_{n} c_{n}>0+b_{n} c_{n}>0
$$
The only thing that we are left to prove is that in the inductive step we may assume that one of the tuples is $a=(0,0, \ldots, 0,-1)$. Fix one of the tuples $x=\left(x_{1}, \ldots, x_{n}\right)$. Set a real number $\varphi$ for which $\tan \varphi=\frac{x_{1}}{x_{2}}$. Change each tuple $a=\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ (including $x$ ), to the tuple
$$
\left(a_{1} \cos \varphi-a_{2} \sin \varphi, a_{1} \sin \varphi+a_{2} \cos \varphi, a_{3}, a_{4}, \ldots, a_{n}\right)
$$
A straightforward calculation shows that the first coordinate of the tuple $x$ becomes 0 , and that all the expressions of the form $a_{1} b_{1}+\cdots+a_{n} b_{n}$ are preserved. We may iterate this process until all the entries of $x$ except for the last one are equal to 0 . We finish by multiplying all the entries in all the tuples by a suitable constant that makes the last entry of $x$ equal to -1 . This preserves the sign of all the expressions of the form $a_{1} b_{1}+\cdots+a_{n} b_{n}$.
We proceed to the proof of our claim. Let $A$ be a set of non-zero tuples among which any two form an exquisite pair. It suffices to prove that $|A| \leq n^{2}+n$. We can write $A$ as a disjoint union of subsets $A_{1} \cup A_{2} \cup \ldots \cup A_{n}$, where $A_{i}$ is the set of tuples in $A$ whose last non-zero entry appears in the $i$ th position. We will show that $\left|A_{i}\right| \leq 2 i$, which will finish our proof since $2+4+\cdots+2 n=n^{2}+n$.
Proceeding by contradiction, suppose that $\left|A_{i}\right| \geq 2 i+1$. If $A_{i}$ has three or more tuples whose only non-zero entry is in the $i$ th position, then for two of them this entry has the same sign. Since the tuples are different and their entries are integers, this yields two tuples for which $\left|\sum a_{i} b_{i}\right| \geq 2$, a contradiction. So there are at most two such tuples. We remove them from $A_{i}$.
Now, for each of the remaining tuples $a$, if it has a positive $i$ th coordinate, we keep $a$ as it is. If it has a negative $i$ th coordinate, we replace it with the opposite tuple $-a$ with entries with opposite signs. This does not changes the exquisite pairs condition.
After making the necessary changes, we have two cases. The first case is that there are two tuples $a$ and $b$ that have the same first $i-1$ coordinates and thus
$$
a_{1} b_{1}+\cdots+a_{i-1} b_{i-1}=a_{1}^{2}+\cdots+a_{i-1}^{2}>0
$$
and thus is at least 1 (the entries are integers). The second case is that no two tuples have the same first $i-1$ coordinates, but then by the Lemma we find two tuples $a$ and $b$ for which
$$
a_{1} b_{1}+\cdots+a_{i-1} b_{i-1} \geq 1
$$
In any case, we obtain
$$
a_{1} b_{1}+\cdots+a_{i-1} b_{i-1}+a_{i} b_{i} \geq 2
$$
This yields a final contradiction to the exquisite pair hypothesis.
|
{
"problem_match": "\nProblem 5.",
"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl",
"solution_match": "\nSolution."
}
| 137
| 1,705
|
2018
|
T1
|
1
| null |
APMO
|
Let $H$ be the orthocenter of the triangle $A B C$. Let $M$ and $N$ be the midpoints of the sides $A B$ and $A C$, respectively. Assume that $H$ lies inside the quadrilateral $B M N C$ and that the circumcircles of triangles $B M H$ and $C N H$ are tangent to each other. The line through $H$ parallel to $B C$ intersects the circumcircles of the triangles $B M H$ and $C N H$ in the points $K$ and $L$, respectively. Let $F$ be the intersection point of $M K$ and $N L$ and let $J$ be the incenter of triangle $M H N$. Prove that $F J=F A$.
|
Lemma 1. In a triangle $A B C$, let $D$ be the intersection of the interior angle bisector at $A$ with the circumcircle of $A B C$, and let $I$ be the incenter of $\triangle A B C$. Then
$$
D I=D B=D C
$$
Proof.
$$
\angle D B I=\frac{\angle B A C}{2}+\frac{\widehat{B}}{2}=\angle D I B \quad \Rightarrow \quad D I=D B
$$
Analogously $D I=D C$.
We start solving the problem. First we state some position considerations. Since there is an arc of the circumcircle of $B H M$ outside the triangle $A B C$, it must happen that $K$ and $N$ lie on opposite sides of $A M$. Similarly, $L$ and $M$ lie on opposite sides of $A N$. Also, $K$ and $L$ lie on the same side of $M N$, and opposite to $A$. Therefore, $F$ lies inside the triangle $A M N$.
Now, since $H$ is the orthocenter of $\triangle A B C$ and the circumcircles of $B M H$ and $C N H$ are tangent we have
$$
\angle A B H=90^{\circ}-\angle B A C=\angle A C H \quad \Rightarrow \quad \angle M H N=\angle M B H+\angle N C H=180^{\circ}-2 \angle B A C .
$$
So $\angle M B H=\angle M K H=\angle N C H=\angle N L H=90^{\circ}-\angle B A C$ and, since $M N \| K L$, we have
$$
\angle F M N=\angle F N M=90^{\circ}-\angle B A C \Rightarrow \angle M F N=2 \angle B A C .
$$
The relations (1) and (2) yield that the quadrilateral $M F N H$ is cyclic, with the vertices in this order around the circumference. Since $F M=F N, \angle M F N=2 \angle B A C$ and $F$ is the correct side of $M N$ we have that the point $F$ is the circumcenter of triangle $A M N$, and thus $F A=F M=F N$.
Since the quadrilateral $M F N H$ is cyclic, $F M=F N$ and $H$ lies on the correct side of $M N$, we have that $H, J$ and $F$ are collinear. According to Lemma $1, F J=F M=F N$. So $F J=F A$.
|
{
"problem_match": "\nProblem 1.",
"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl",
"solution_match": "# Solution."
}
| 170
| 595
|
2018
|
T1
|
2
| null |
APMO
|
Let $f(x)$ and $g(x)$ be given by
$$
f(x)=\frac{1}{x}+\frac{1}{x-2}+\frac{1}{x-4}+\cdots+\frac{1}{x-2018}
$$
and
$$
g(x)=\frac{1}{x-1}+\frac{1}{x-3}+\frac{1}{x-5}+\cdots+\frac{1}{x-2017} .
$$
Prove that
$$
|f(x)-g(x)|>2
$$
for any non-integer real number $x$ satisfying $0<x<2018$.
|
There are two cases: $2 n-1<x<2 n$ and $2 n<x<2 n+1$. Note that $f(2018-x)=-f(x)$ and $g(2018-x)=-g(x)$, that is, a half turn about the point $(1009,0)$ preserves the graphs of $f$ and $g$. So it suffices to consider only the case $2 n-1<x<2 n$.
Let $d(x)=g(x)-f(x)$. We will show that $d(x)>2$ whenever $2 n-1<x<2 n$ and $n \in\{1,2, \ldots, 1009\}$.
For any non-integer $x$ with $0<x<2018$, we have
$$
d(x+2)-d(x)=\left(\frac{1}{x+1}-\frac{1}{x+2}\right)+\left(\frac{1}{x-2018}-\frac{1}{x-2017}\right)>0+0=0
$$
Hence it suffices to prove $d(x)>2$ for $1<x<2$. Since $x<2$, it follows that $\frac{1}{x-2 i-1}>$ $\frac{1}{x-2 i}$ for $i=2,3, \ldots, 1008$. We also have $\frac{1}{x-2018}<0$. Hence it suffices to prove the following
for $1<x<2$.
$$
\begin{aligned}
& \frac{1}{x-1}+\frac{1}{x-3}-\frac{1}{x}-\frac{1}{x-2}>2 \\
\Leftrightarrow & \left(\frac{1}{x-1}+\frac{1}{2-x}\right)+\left(\frac{1}{x-3}-\frac{1}{x}\right)>2 \\
\Leftrightarrow & \frac{1}{(x-1)(2-x)}+\frac{3}{x(x-3)}>2 .
\end{aligned}
$$
By the $G M-H M$ inequality (alternatively, by considering the maximum of the quadratic $(x-1)(2-x))$ we have
$$
\frac{1}{x-1} \cdot \frac{1}{2-x}>\left(\frac{2}{(x-1)+(2-x)}\right)^{2}=4
$$
To find a lower bound for $\frac{3}{x(x-3)}$, note that $x(x-3)<0$ for $1<x<2$. So we seek an upper bound for $x(x-3)$. From the shape of the quadratic, this occurs at $x=1$ or $x=2$, both of which yield $\frac{3}{x(x-3)}>-\frac{3}{2}$.
It follows that $d(x)>4-\frac{3}{2}>2$, as desired.
|
{
"problem_match": "\nProblem 2.",
"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl",
"solution_match": "\nSolution 1"
}
| 151
| 671
|
2018
|
T1
|
2
| null |
APMO
|
Let $f(x)$ and $g(x)$ be given by
$$
f(x)=\frac{1}{x}+\frac{1}{x-2}+\frac{1}{x-4}+\cdots+\frac{1}{x-2018}
$$
and
$$
g(x)=\frac{1}{x-1}+\frac{1}{x-3}+\frac{1}{x-5}+\cdots+\frac{1}{x-2017} .
$$
Prove that
$$
|f(x)-g(x)|>2
$$
for any non-integer real number $x$ satisfying $0<x<2018$.
|
As in Solution 1, we may assume $2 n-1<x<2 n$ for some $1 \leq n \leq 1009$. Let $d(x)=$ $f(x)-g(x)$, and note that
$$
d(x)=\frac{1}{x}+\sum_{m=1}^{1009} \frac{1}{(x-2 m)(x-2 m+1)}
$$
We split the sum into three parts: the terms before $m=n$, after $m=n$, and the term $m=n$. The first two are
$$
\begin{aligned}
0 & \leq \sum_{m=1}^{n-1} \frac{1}{(x-2 m)(x-2 m+1)} \\
& \leq \sum_{m=1}^{n-1} \frac{1}{(2 n-1-2 m)(2 n-2 m)}=\sum_{i=1}^{n-1} \frac{1}{(2 i)(2 i-1)} \leq \sum_{i=1}^{1008} \frac{1}{2 i-1}-\frac{1}{2 i} \\
0 & \leq \sum_{m=n+1}^{1009} \frac{1}{(2 m-x)(2 m-1-x)} \\
& \leq \sum_{m=n+1}^{1009} \frac{1}{(2 m-2 n+1)(2 m-2 n)}=\sum_{i=1}^{1009-n} \frac{1}{(2 i+1)(2 i)} \leq \sum_{i=1}^{1008} \frac{1}{2 i}-\frac{1}{2 i+1} .
\end{aligned}
$$
When we add the two sums the terms telescope and we are left with
$$
0 \leq \sum_{1 \leq m \leq 1009, m \neq n} \frac{1}{(x-2 m)(x-2 m+1)} \leq 1-\frac{1}{2017}<1
$$
For the term $m=n$, we write
$$
0<-(x-2 n)(x-2 n+1)=0.25-(x-2 n+0.5)^{2} \leq 0.25
$$
whence
$$
-4 \geq \frac{1}{(x-2 n)(x-2 n+1)}
$$
Finally, $\frac{1}{x}<1$ since $x>2 n-1 \geq 1$. Combining these we get
$$
d(x)=\frac{1}{x}+\sum_{m=1}^{1009} \frac{1}{(x-2 m)(x-2 m+1)}<1+1-4<-2 .
$$
|
{
"problem_match": "\nProblem 2.",
"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl",
"solution_match": "# Solution 2"
}
| 151
| 665
|
2018
|
T1
|
3
| null |
APMO
|
A collection of $n$ squares on the plane is called tri-connected if the following criteria are satisfied:
(i) All the squares are congruent.
(ii) If two squares have a point $P$ in common, then $P$ is a vertex of each of the squares.
(iii) Each square touches exactly three other squares.
How many positive integers $n$ are there with $2018 \leq n \leq 3018$, such that there exists a collection of $n$ squares that is tri-connected?
Answer: 501
|
We will prove that there is no tri-connected collection if $n$ is odd, and that tri-connected collections exist for all even $n \geq 38$. Since there are 501 even numbers in the range from 2018 to 3018, this yields 501 as the answer.
For any two different squares $A$ and $B$, let us write $A \sim B$ to mean that square $A$ touches square $B$. Since each square touches exactly three other squares, and there are $n$ squares in total, the total number of instances of $A \sim B$ is $3 n$. But $A \sim B$ if and only if $B \sim A$. Hence the total number of instances of $A \sim B$ is even. Thus $3 n$ and hence also $n$ is even.
We now construct tri-connected collections for each even $n$ in the range. We show two
Construction 1 The idea is to use the following two configurations. Observe that in each configuration every square is related to three squares except for the leftmost and rightmost squares which are related to two squares. Note that the configuration on the left is of variable length. Also observe that multiple copies of the configuration on the right can be chained together to end around corners.
Putting the above two types of configurations together as in the following figure yields a tri-connected collection for every even $n \geq 38$.
Construction 2 Consider a regular $4 n$-gon $A_{1} A_{2} \cdots A_{4 n}$, and make $4 n$ squares on the outside of the $4 n$-gon with one side being on the $4 n$-gon. Reflect squares sharing sides $A_{4 m+2} A_{4 m+3}, A_{4 m+3} A_{4 m+4}$ across line $A_{4 m+2} A_{4 m+4}$, for $0 \leq m \leq n-1$. This will produce a tri-connected set of $6 n$ squares, as long as the squares inside the $4 n$-gon do not intersect. When $n \geq 4$, this will be true. The picture for $n=24$ is as follows:
To treat the other cases, consider the following gadget
Two squares touch 3 other squares, and the squares containing $X, Y$ touch 2 other squares. Take the $4 n$-gon from above, and break it into two along the line $A_{1} A_{2 n}$, moving the two parts away from that line. Do so until the gaps can be exactly filled by inserting two copies of the above figure, so that the vertices $X, Y$ touch the two vertices which used to be $A_{1}$ in one instance, and the two vertices which used to be $A_{2 n}$ in the other.
This gives us a valid configuration for $6 n+8$ squares, $n \geq 4$. Finally, if we had instead spread the two parts out more and inserted two copies of the above figure into each gap, we would get $6 n+16$ for $n \geq 4$, which finishes the proof for all even numbers at least 36 .
|
{
"problem_match": "\nProblem 3.",
"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl",
"solution_match": "\nSolution."
}
| 118
| 710
|
2018
|
T1
|
4
| null |
APMO
|
Let $A B C$ be an equilateral triangle. From the vertex $A$ we draw a ray towards the interior of the triangle such that the ray reaches one of the sides of the triangle. When the ray reaches a side, it then bounces off following the law of reflection, that is, if it arrives with a directed angle $\alpha$, it leaves with a directed angle $180^{\circ}-\alpha$. After $n$ bounces, the ray returns to $A$ without ever landing on any of the other two vertices. Find all possible values of $n$.
Answer: All $n \equiv 1,5 \bmod 6$ with the exception of 5 and 17
|
Consider an equilateral triangle $A A_{1} A_{2}$ of side length $m$ and triangulate it with unitary triangles. See the figure. To each of the vertices that remain after the triangulation we can assign a pair of coordinates $(a, b)$ where $a, b$ are non-negative integers, $a$ is the number of edges we travel in the $A A_{1}$ direction and $b$ is the number of edges we travel in the $A A_{2}$ direction to arrive to the vertex, (we have $A=(0,0), A_{1}=(m, 0)$ and $A_{2}=(0, m)$ ). The unitary triangle with vertex $A$ will be our triangle $A B C,(B=(1,0), C=(0,1))$. We can obtain every unitary triangle by starting with $A B C$ and performing reflections with respect to a side (the vertex $(1,1)$ is the reflection of $A$ with respect to $B C$, the vertex $(0,2)$ is the reflection of $B=(1,0)$ with respect to the side formed by $C=(1,0)$ and $(1,1)$, and so on).
When we reflect a vertex $(a, b)$ with respect to a side of one of the triangles, the congruence of $a-b$ is preserved modulo 3. Furthermore, an induction argument shows that any two vertices $(a, b)$ and $\left(a^{\prime}, b^{\prime}\right)$ with $a-b \equiv a^{\prime}-b^{\prime}$ mod 3 can be obtained from each other by a series of such reflections. Therefore, the set of vertices $V$ that result from the reflections of $A$ will be those of the form $(a, b)$ satisfying $a \equiv b \bmod 3$. See the green vertices in the figure.
Now, let $U$ be the set of vertices $u$ that satisfy that the line segment between $u$ and $A$ does not pass through any other vertex. A pair $(a, b)$ is in $U$ if and only if $\operatorname{gcd}(a, b)=1$, since otherwise for $d=\operatorname{gcd}(a, b)$ we have that the vertex $(a / d, b / d)$ also lies on the line segment between $u$ and $A$.
Observe that the rays that come out from $A$ and eventually return to $A$ are those that come out towards a vertex in $V \cap U$ (they would be in $V$ to be able to come back to $A$ and in $U$ so that they do not reach a vertex beforehand). In the diagram, a ray toward one such vertex $(a, b)$ will intersect exactly $(a-1)+(b-1)+(a+b-1)=2(a+b)-3$ lines: $a-1$ of them parallel to $A B, b-1$ parallel to $A C$ and $a+b-1$ parallel to $B C$. Therefore, in the triangle $A B C$ the ray will bounce $2(a+b)-3$ times before returning to $A$. So we want to find all
$n=2(a+b)-3$ where $a \equiv b \bmod 3$ and $\operatorname{gcd}(a, b)=1$.
If $a+b$ is a multiple of 3 then we cannot satisfy both conditions simultaneously, therefore $n$ is not a multiple of 3 . We also know that $n$ is odd. Therefore $n \equiv 1,5,7,11 \bmod 12$. Note that the pair $(1,3 k+1)$ satisfies the conditions and we can create $n=2(3 k+2)-3=6 k+1$ for all $k \geq 0$ (this settles the question for $n \equiv 1,7 \bmod 12$ ). For $n \equiv 5 \bmod 12$ consider the pair $(3 k-1,3 k+5)$ when $k$ is even or $(3 k-4,3 k+8)$ when $k$ is odd. This gives us all the integers of the form $12 k+5$ for $k \geq 2$. For $11 \bmod 12$, take the pairs $(3 k-1,3 k+2)($ with $k \geq 1)$, which yield all positive integers of the form $12 k-1$.
Finally, to discard 5 and 17 note that the only pairs $(a, b)$ that are solutions to $2(a+b)-3=5$ or $2(a+b)-3=17$ with the same residue $\bmod 3$ in this range are the non-relatively prime pairs $(2,2),(2,8)$ and $(5,5)$.
|
{
"problem_match": "\nProblem 4.",
"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl",
"solution_match": "\nSolution."
}
| 150
| 1,071
|
2018
|
T1
|
5
| null |
APMO
|
Find all polynomials $P(x)$ with integer coefficients such that for all real numbers $s$ and $t$, if $P(s)$ and $P(t)$ are both integers, then $P(s t)$ is also an integer.
Answer: $P(x)=x^{n}+k,-x^{n}+k$ for $n$ a non-negative integer and $k$ an integer.
|
: $P(x)=x^{n}+k,-x^{n}+k$ for $n$ a non-negative integer and $k$ an integer.
Notice that if $P(x)$ is a solution, then so is $P(x)+k$ and $-P(x)+k$ for any integer $k$, so we may assume that the leading coefficient of $P(x)$ is positive and that $P(0)=0$, i.e., we can assume that $P(x)=\sum_{i=1}^{n} a_{i} x^{i}$ with $a_{n}>0$. We are going to prove that $P(x)=x^{n}$ in this case.
Let $p$ be a large prime such that $p>\sum_{i=1}^{n}\left|a_{i}\right|$. Because $P$ has a positive leading coefficient and $p$ is large enough, we can find $t \in \mathbb{R}$ such that $P(t)=p$. Denote the greatest common divisor of the polynomial $P(x)-p$ and $P(2 x)-P(2 t)$ as $f(x)$, and $t$ is a root of it, so $f$ is a non-constant polynomial. Notice that $P(2 t)$ is an integer by using the hypothesis for $s=2$ and $t$. Since $P(x)-p$ and $P(2 x)-P(2 t)$ are polynomials with integer coefficients, $f$ can be chosen as a polynomial with rational coefficients.
In the following, we will prove that $f$ is the same as $P(x)-p$ up to a constant multiplier. Say $P(x)-p=f(x) g(x)$, where $f$ and $g$ are non-constant polynomials. By Gauss's lemma, we can get $f_{1}, g_{1}$ with $P(x)-p=f_{1}(x) g_{1}(x)$ where $f_{1}$ is a scalar multiple of $f$ and $g_{1}$ is a scalar multiple of $g$ and one of $f_{1}, g_{1}$ has constant term $\pm 1$ (this is because $-p=P(0)-p=f(0) g(0)$ with $p$ prime). So $P(x)-p$ has at least one root $r$ with absolute value not greater than 1 (using
Vieta, the product of the roots of the polynomial with constant term $\pm 1$ is $\pm 1$ ), but
$$
|P(r)-p|=\left|\sum_{i=1}^{n} a_{i} r^{i}-p\right|>p-\sum_{i=1}^{n}\left|a_{i}\right|>0
$$
hence we get a contradiction!
Therefore $f$ is a constant multiple of $P(x)-p$, so $P(2 x)-P(2 t)$ is a constant multiple of $P(x)-p$ because they both have the same degree. By comparing leading coefficients we get that $P(2 x)-P(2 t)=2^{n}(P(x)-p)$. Comparing the rest of the coefficients we get that $P(x)=a_{n} x^{n}$. If we let $a=b=\left(1 / a_{n}\right)^{1 / n}$, then $P(a)=P(b)=1$, so $P(a b)$ must also be an integer. But $P(a b)=\frac{1}{a_{n}}$. Therefore $a_{n}=1$ and the proof is complete.
|
{
"problem_match": "\nProblem 5.",
"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl",
"solution_match": "\nSolution 1"
}
| 84
| 788
|
2018
|
T1
|
5
| null |
APMO
|
Find all polynomials $P(x)$ with integer coefficients such that for all real numbers $s$ and $t$, if $P(s)$ and $P(t)$ are both integers, then $P(s t)$ is also an integer.
Answer: $P(x)=x^{n}+k,-x^{n}+k$ for $n$ a non-negative integer and $k$ an integer.
|
: Assume $P(x)=\sum_{i=0}^{n} a_{i} x^{i}$. Consider the following system of equations
$$
\begin{aligned}
& a_{0}=P(0) \\
& a_{n} t^{n}+a_{n-1} t^{n-1}+\cdots+a_{0}=P(t) \\
& 2^{n} a_{n} t^{n}+2^{n-1} a_{n-1} t^{n-1}+\cdots+a_{0}=P(2 t) \\
& \vdots \\
& n^{n} a_{n} t^{n}+n^{n-1} a_{n-1} t^{n-1}+\cdots+a_{0}=P(n t)
\end{aligned}
$$
viewing $a_{k} t^{k}$ as variables. Note that if $P(t)$ is an integer, then by the hypothesis all the terms on the right hand side of the equations are integers as well. By using Cramer's rule, we can get that $a_{k} t^{k}=D / M$, where $D$ is an integer and $M$ is the following determinant
$$
\left|\begin{array}{ccccc}
1 & 0 & 0 & \cdots & 0 \\
1 & 1 & 1 & \cdots & 1 \\
1 & 2 & 4 & \cdots & 2^{n} \\
\vdots & \vdots & \vdots & & \vdots \\
1 & n & n^{2} & \cdots & n^{n}
\end{array}\right| \neq 0
$$
Thus, if we let $r$ be the smallest positive index such that $a_{r} \neq 0$, we can express each $t \in \mathbb{R}$ with $P(t) \in \mathbb{Z}$ in the form $\left(\frac{m}{M^{\prime}}\right)^{1 / r}$ for some integer $m$, and where $M^{\prime}=M \times a_{r}$ is a constant.
We can choose $L$ large enough such that $\left.P\right|_{\mathbb{R}_{\geq L}}$ is injective, and for any larger $N$, the growth order of the number of values in the form $\left(\frac{m}{M^{\prime}}\right)^{1 / r}$ is $N^{r}$, while the growth order of the number of integers in $[P(L), P(N)]$ is $N^{n}$, so $r=n$. Therefore $P(x)$ is of the form $a_{n} x^{n}+k$. The problem can be finished as in Solution 1.
|
{
"problem_match": "\nProblem 5.",
"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl",
"solution_match": "\nSolution 2"
}
| 84
| 619
|
2019
|
T1
|
1
| null |
APMO
|
Let $\mathbb{Z}^{+}$be the set of positive integers. Determine all functions $f: \mathbb{Z}^{+} \rightarrow \mathbb{Z}^{+}$ such that $a^{2}+f(a) f(b)$ is divisible by $f(a)+b$ for all positive integers $a$ and $b$.
Answer: The answer is $f(n)=n$ for all positive integers $n$.
Clearly, $f(n)=n$ for all $n \in \mathbb{Z}^{+}$satisfies the original relation. We show some possible approaches to prove that this is the only possible function.
|
: As above, we have relations (1)-(3). In (2) and (3), for $b=2$ we have $3 \mid f(2)+1$ and $f(2)+1 \mid 3$. These imply $f(2)=2$.
Now, using $a=2$ we get $2+b \mid 4+2 f(b)$. Let $f(b)=x$. We have
$$
\begin{aligned}
1+x & \equiv 0 \quad(\bmod b+1) \\
4+2 x & \equiv 0 \quad(\bmod b+2)
\end{aligned}
$$
From the first equation $x \equiv b(\bmod b+1)$ so $x=b+(b+1) t$ for some integer $t \geq 0$. Then
$$
0 \equiv 4+2 x \equiv 4+2(b+(b+1) t) \equiv 4+2(-2-t) \equiv-2 t \quad(\bmod b+2)
$$
Also $t \leq b-2$ because $1+x \mid b^{2}-1$ by (3).
If $b+2$ is odd, then $t \equiv 0(\bmod b+2)$. Then $t=0$, which implies $f(b)=b$.
If $b+2$ is even, then $t \equiv 0(\bmod (b+2) / 2)$. Then $t=0$ or $t=(b+2) / 2$. But if $t \neq 0$, then by definition $(b+4) / 2=(1+t)=(x+1) /(b+1)$ and since $x+1 \mid b^{2}-1$, then $(b+4) / 2$ divides $b-1$. Therefore $b+4 \mid 10$ and the only possibility is $b=6$. So for even $b, b \neq 6$ we have $f(b)=b$.
Finally, by (2) and (3), for $b=6$ we have $7 \mid f(6)+1$ and $f(6)+1 \mid 35$. This means $f(6)=6$ or $f(6)=34$. The later is discarded as, for $a=5, b=6$, we have by the original equation that $11 \mid 5(5+f(6))$. Therefore $f(n)=n$ for every positive integer $n$.
|
{
"problem_match": "\nProblem 1.",
"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl",
"solution_match": "\nSolution 2"
}
| 142
| 561
|
2019
|
T1
|
2
| null |
APMO
|
Let $m$ be a fixed positive integer. The infinite sequence $\left\{a_{n}\right\}_{n \geq 1}$ is defined in the following way: $a_{1}$ is a positive integer, and for every integer $n \geq 1$ we have
$$
a_{n+1}= \begin{cases}a_{n}^{2}+2^{m} & \text { if } a_{n}<2^{m} \\ a_{n} / 2 & \text { if } a_{n} \geq 2^{m}\end{cases}
$$
For each $m$, determine all possible values of $a_{1}$ such that every term in the sequence is an integer.
Answer: The only value of $m$ for which valid values of $a_{1}$ exist is $m=2$. In that case, the only solutions are $a_{1}=2^{\ell}$ for $\ell \geq 1$.
|
Suppose that for integers $m$ and $a_{1}$ all the terms of the sequence are integers. For each $i \geq 1$, write the $i$ th term of the sequence as $a_{i}=b_{i} 2^{c_{i}}$ where $b_{i}$ is the largest odd divisor of $a_{i}$ (the "odd part" of $a_{i}$ ) and $c_{i}$ is a nonnegative integer.
Lemma 1. The sequence $b_{1}, b_{2}, \ldots$ is bounded above by $2^{m}$.
Proof. Suppose this is not the case and take an index $i$ for which $b_{i}>2^{m}$ and for which $c_{i}$ is minimal. Since $a_{i} \geq b_{i}>2^{m}$, we are in the second case of the recursion. Therefore, $a_{i+1}=a_{i} / 2$ and thus $b_{i+1}=b_{i}>2^{m}$ and $c_{i+1}=c_{i}-1<c_{i}$. This contradicts the minimality of $c_{i}$.
Lemma 2. The sequence $b_{1}, b_{2}, \ldots$ is nondecreasing.
Proof. If $a_{i} \geq 2^{m}$, then $a_{i+1}=a_{i} / 2$ and thus $b_{i+1}=b_{i}$. On the other hand, if $a_{i}<2^{m}$, then
$$
a_{i+1}=a_{i}^{2}+2^{m}=b_{i}^{2} 2^{2 c_{i}}+2^{m}
$$
and we have the following cases:
- If $2 c_{i}>m$, then $a_{i+1}=2^{m}\left(b_{i}^{2} 2^{2 c_{i}-m}+1\right)$, so $b_{i+1}=b_{i}^{2} 2^{2 c_{i}-m}+1>b_{i}$.
- If $2 c_{i}<m$, then $a_{i+1}=2^{2 c_{i}}\left(b_{i}^{2}+2^{m-2 c_{i}}\right)$, so $b_{i+1}=b_{i}^{2}+2^{m-2 c_{i}}>b_{i}$.
- If $2 c_{i}=m$, then $a_{i+1}=2^{m+1} \cdot \frac{b_{i}^{2}+1}{2}$, so $b_{i+1}=\left(b_{i}^{2}+1\right) / 2 \geq b_{i}$ since $b_{i}^{2}+1 \equiv 2(\bmod 4)$.
By combining these two lemmas we obtain that the sequence $b_{1}, b_{2}, \ldots$ is eventually constant. Fix an index $j$ such that $b_{k}=b_{j}$ for all $k \geq j$. Since $a_{n}$ descends to $a_{n} / 2$ whenever $a_{n} \geq 2^{m}$, there are infinitely many terms which are smaller than $2^{m}$. Thus, we can choose an $i>j$ such that $a_{i}<2^{m}$. From the proof of Lemma $2, a_{i}<2^{m}$ and $b_{i+1}=b_{i}$ can happen simultaneously only when $2 c_{i}=m$ and $b_{i+1}=b_{i}=1$. By Lemma 2 , the sequence $b_{1}, b_{2}, \ldots$ is constantly 1 and thus $a_{1}, a_{2}, \ldots$ are all powers of two. Tracing the sequence starting from $a_{i}=2^{c_{i}}=2^{m / 2}<2^{m}$,
$$
2^{m / 2} \rightarrow 2^{m+1} \rightarrow 2^{m} \rightarrow 2^{m-1} \rightarrow 2^{2 m-2}+2^{m}
$$
Note that this last term is a power of two if and only if $2 m-2=m$. This implies that $m$ must be equal to 2 . When $m=2$ and $a_{1}=2^{\ell}$ for $\ell \geq 1$ the sequence eventually cycles through $2,8,4,2, \ldots$. When $m=2$ and $a_{1}=1$ the sequence fails as the first terms are $1,5,5 / 2$.
|
{
"problem_match": "\nProblem 2.",
"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl",
"solution_match": "\nSolution."
}
| 213
| 1,067
|
2019
|
T1
|
2
| null |
APMO
|
Let $m$ be a fixed positive integer. The infinite sequence $\left\{a_{n}\right\}_{n \geq 1}$ is defined in the following way: $a_{1}$ is a positive integer, and for every integer $n \geq 1$ we have
$$
a_{n+1}= \begin{cases}a_{n}^{2}+2^{m} & \text { if } a_{n}<2^{m} \\ a_{n} / 2 & \text { if } a_{n} \geq 2^{m}\end{cases}
$$
For each $m$, determine all possible values of $a_{1}$ such that every term in the sequence is an integer.
Answer: The only value of $m$ for which valid values of $a_{1}$ exist is $m=2$. In that case, the only solutions are $a_{1}=2^{\ell}$ for $\ell \geq 1$.
|
: Let $m$ be a positive integer and suppose that $\left\{a_{n}\right\}$ consists only of positive integers. Call a number small if it is smaller than $2^{m}$ and large otherwise. By the recursion,
after a small number we have a large one and after a large one we successively divide by 2 until we get a small one.
First, we note that $\left\{a_{n}\right\}$ is bounded. Indeed, $a_{1}$ turns into a small number after a finite number of steps. After this point, each small number is smaller than $2^{m}$, so each large number is smaller than $2^{2 m}+2^{m}$. Now, since $\left\{a_{n}\right\}$ is bounded and consists only of positive integers, it is eventually periodic. We focus only on the cycle.
Any small number $a_{n}$ in the cycle can be writen as $a / 2$ for $a$ large, so $a_{n} \geq 2^{m-1}$, then $a_{n+1} \geq 2^{2 m-2}+2^{m}=2^{m-2}\left(4+2^{m}\right)$, so we have to divide $a_{n+1}$ at least $m-1$ times by 2 until we get a small number. This means that $a_{n+m}=\left(a_{n}^{2}+2^{m}\right) / 2^{m-1}$, so $2^{m-1} \mid a_{n}^{2}$, and therefore $2^{\lceil(m-1) / 2\rceil} \mid a_{n}$ for any small number $a_{n}$ in the cycle. On the other hand, $a_{n} \leq 2^{m}-1$, so $a_{n+1} \leq 2^{2 m}-2^{m+1}+1+2^{m} \leq 2^{m}\left(2^{m}-1\right)$, so we have to divide $a_{n+1}$ at most $m$ times by two until we get a small number. This means that after $a_{n}$, the next small number is either $N=a_{m+n}=\left(a_{n}^{2} / 2^{m-1}\right)+2$ or $a_{m+n+1}=N / 2$. In any case, $2^{\lceil(m-1) / 2\rceil}$ divides $N$.
If $m$ is odd, then $x^{2} \equiv-2\left(\bmod 2^{\lceil(m-1) / 2\rceil}\right)$ has a solution $x=a_{n} / 2^{(m-1) / 2}$. If $(m-1) / 2 \geq$ $2 \Longleftrightarrow m \geq 5$ then $x^{2} \equiv-2(\bmod 4)$, which has no solution. So if $m$ is odd, then $m \leq 3$.
If $m$ is even, then $2^{m-1}\left|a_{n}^{2} \Longrightarrow 2^{\lceil(m-1) / 2\rceil}\right| a_{n} \Longleftrightarrow 2^{m / 2} \mid a_{n}$. Then if $a_{n}=2^{m / 2} x$, $2 x^{2} \equiv-2\left(\bmod 2^{m / 2}\right) \Longleftrightarrow x^{2} \equiv-1\left(\bmod 2^{(m / 2)-1}\right)$, which is not possible for $m \geq 6$. So if $m$ is even, then $m \leq 4$.
The cases $m=1,2,3,4$ are handed manually, checking the possible small numbers in the cycle, which have to be in the interval $\left[2^{m-1}, 2^{m}\right)$ and be divisible by $2^{\lceil(m-1) / 2\rceil}$ :
- For $m=1$, the only small number is 1 , which leads to 5 , then $5 / 2$.
- For $m=2$, the only eligible small number is 2 , which gives the cycle $(2,8,4)$. The only way to get to 2 is by dividing 4 by 2 , so the starting numbers greater than 2 are all numbers that lead to 4 , which are the powers of 2 .
- For $m=3$, the eligible small numbers are 4 and 6 ; we then obtain $4,24,12,6,44,22,11,11 / 2$.
- For $m=4$, the eligible small numbers are 8 and 12 ; we then obtain $8,80,40,20,10, \ldots$ or $12,160,80,40,20,10, \ldots$, but in either case 10 is not an elegible small number.
|
{
"problem_match": "\nProblem 2.",
"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl",
"solution_match": "\nSolution 2"
}
| 213
| 1,165
|
2019
|
T1
|
3
| null |
APMO
|
Let $A B C$
be a scalene triangle with circumcircle $\Gamma$. Let $M$ be the midpoint of $B C$. A variable point $P$ is selected in the line segment $A M$. The circumcircles of triangles $B P M$ and $C P M$ intersect $\Gamma$ again at points $D$ and $E$, respectively. The lines $D P$ and $E P$ intersect (a second time) the circumcircles to triangles $C P M$ and $B P M$ at $X$ and $Y$, respectively. Prove that as $P$ varies, the circumcircle of $\triangle A X Y$ passes through a fixed point $T$ distinct from $A$.
|
Let $N$ be the radical center of the circumcircles of triangles $A B C, B M P$ and $C M P$. The pairwise radical axes of these circles are $B D, C E$ and $P M$, and hence they concur at $N$. Now, note that in directed angles:
$$
\angle M C E=\angle M P E=\angle M P Y=\angle M B Y .
$$
It follows that $B Y$ is parallel to $C E$, and analogously that $C X$ is parallel to $B D$. Then, if $L$ is the intersection of $B Y$ and $C X$, it follows that $B N C L$ is a parallelogram. Since $B M=M C$ we deduce that $L$ is the reflection of $N$ with respect to $M$, and therefore $L \in A M$. Using power of a point from $L$ to the circumcircles of triangles $B P M$ and $C P M$, we have
$$
L Y \cdot L B=L P \cdot L M=L X \cdot L C
$$
Hence, $B Y X C$ is cyclic. Using the cyclic quadrilateral we find in directed angles:
$$
\angle L X Y=\angle L B C=\angle B C N=\angle N D E .
$$
Since $C X \| B N$, it follows that $X Y \| D E$.
Let $Q$ and $R$ be two points in $\Gamma$ such that $C Q, B R$, and $A M$ are all parallel. Then in directed angles:
$$
\angle Q D B=\angle Q C B=\angle A M B=\angle P M B=\angle P D B .
$$
Then $D, P, Q$ are collinear. Analogously $E, P, R$ are collinear. From here we get $\angle P R Q=$ $\angle P D E=\angle P X Y$, since $X Y$ and $D E$ are parallel. Therefore $Q R Y X$ is cyclic. Let $S$ be the radical center of the circumcircle of triangle $A B C$ and the circles $B C Y X$ and $Q R Y X$. This point lies in the lines $B C, Q R$ and $X Y$ because these are the radical axes of the circles. Let $T$ be the second intersection of $A S$ with $\Gamma$. By power of a point from $S$ to the circumcircle of $A B C$ and the circle $B C X Y$ we have
$$
S X \cdot S Y=S B \cdot S C=S T \cdot S A
$$
Therefore $T$ is in the circumcircle of triangle $A X Y$. Since $Q$ and $R$ are fixed regardless of the choice of $P$, then $S$ is also fixed, since it is the intersection of $Q R$ and $B C$. This implies $T$ is also fixed, and therefore, the circumcircle of triangle $A X Y$ goes through $T \neq A$ for any choice of $P$.
Now we show an alternative way to prove that $B C X Y$ and $Q R X T$ are cyclic.
|
{
"problem_match": "# Problem 3.",
"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl",
"solution_match": "\nSolution."
}
| 154
| 703
|
2019
|
T1
|
3
| null |
APMO
|
Let $A B C$
be a scalene triangle with circumcircle $\Gamma$. Let $M$ be the midpoint of $B C$. A variable point $P$ is selected in the line segment $A M$. The circumcircles of triangles $B P M$ and $C P M$ intersect $\Gamma$ again at points $D$ and $E$, respectively. The lines $D P$ and $E P$ intersect (a second time) the circumcircles to triangles $C P M$ and $B P M$ at $X$ and $Y$, respectively. Prove that as $P$ varies, the circumcircle of $\triangle A X Y$ passes through a fixed point $T$ distinct from $A$.
|
. Let the lines $D P$ and $E P$ meet the circumcircle of $A B C$ again at $Q$ and $R$, respectively. Then $\angle D Q C \angle D B C=\angle D P M$, so $Q C \| P M$. Similarly, $R B \| P M$.
Now, $\angle Q C B=\angle P M B=\angle P X C=\angle(Q X, C X)$, which is half of the arc $Q C$ in the circumcircle $\omega_{C}$ of $Q X C$. So $\omega_{C}$ is tangent to $B S$; analogously, $\omega_{B}$, the circumcicle of $R Y B$, is also tangent to $B C$. Since $B R \| C Q$, the inscribed trapezoid $B R Q C$ is isosceles, and by symmetry $Q R$ is also tangent to both circles, and the common perpendicular bisector of $B R$ and $C Q$ passes through the centers of $\omega_{B}$ and $\omega_{C}$. Since $M B=M C$ and $P M\|B R\| C Q$, the line $P M$ is the radical axis of $\omega_{B}$ and $\omega_{C}$.
However, $P M$ is also the radical axis of the circumcircles $\gamma_{B}$ of $P M B$ and $\gamma_{C}$ of $P M C$. Let $C X$ and $P M$ meet at $Z$. Let $p(K, \omega)$ denote the power of a point $K$ with respect to a circumference $\omega$. We have
$$
p\left(Z, \gamma_{B}\right)=p\left(Z, \gamma_{C}\right)=Z X \cdot Z C=p\left(Z, \omega_{B}\right)=p\left(Z, \omega_{C}\right)
$$
Point $Z$ is thus the radical center of $\gamma_{B}, \gamma_{C}, \omega_{B}, \omega_{C}$. Thus, the radical axes $B Y, C X, P M$ meet at $Z$. From here,
$$
\begin{aligned}
& Z Y \cdot Z B=Z C \cdot Z X \Rightarrow B C X Y \text { cyclic } \\
& P Y \cdot P R=P X \cdot P Q \Rightarrow Q R X T \text { cyclic. }
\end{aligned}
$$
We may now finish as in Solution 1.
|
{
"problem_match": "# Problem 3.",
"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl",
"solution_match": "\nSolution 2"
}
| 154
| 547
|
2019
|
T1
|
4
| null |
APMO
|
Consider a $2018 \times 2019$ board with integers in each unit square. Two unit squares are said to be neighbours if they share a common edge. In each turn, you choose some unit squares. Then for each chosen unit square the average of all its neighbours is calculated. Finally, after these calculations are done, the number in each chosen unit square is replaced by the corresponding average. Is it always possible to make the numbers in all squares become the same after finitely many turns?
Answer: No
|
Let $n$ be a positive integer relatively prime to 2 and 3 . We may study the whole process modulo $n$ by replacing divisions by $2,3,4$ with multiplications by the corresponding inverses modulo $n$. If at some point the original process makes all the numbers equal, then the process modulo $n$ will also have all the numbers equal. Our aim is to choose $n$ and an initial configuration modulo $n$ for which no process modulo $n$ reaches a board with all numbers equal modulo $n$. We split this goal into two lemmas.
Lemma 1. There is a $2 \times 3$ board that stays constant modulo 5 and whose entries are not all equal.
Proof. Here is one such a board:
The fact that the board remains constant regardless of the choice of squares can be checked square by square.
Lemma 2. If there is an $r \times s$ board with $r \geq 2, s \geq 2$, that stays constant modulo 5 , then there is also a $k r \times l s$ board with the same property.
Proof. We prove by a case by case analysis that repeateadly reflecting the $r \times s$ with respect to an edge preserves the property:
- If a cell had 4 neighbors, after reflections it still has the same neighbors.
- If a cell with $a$ had 3 neighbors $b, c, d$, we have by hypothesis that $a \equiv 3^{-1}(b+c+d) \equiv$ $2(b+c+d)(\bmod 5)$. A reflection may add $a$ as a neighbor of the cell and now
$$
4^{-1}(a+b+c+d) \equiv 4(a+b+c+d) \equiv 4 a+2 a \equiv a \quad(\bmod 5)
$$
- If a cell with $a$ had 2 neighbors $b, c$, we have by hypothesis that $a \equiv 2^{-1}(b+c) \equiv 3(b+c)$ $(\bmod 5)$. If the reflections add one $a$ as neighbor, now
$$
3^{-1}(a+b+c) \equiv 2(3(b+c)+b+c) \equiv 8(b+c) \equiv 3(b+c) \equiv a \quad(\bmod 5)
$$
- If a cell with $a$ had 2 neighbors $b, c$, we have by hypothesis that $a \equiv 2^{-1}(b+c)(\bmod 5)$. If the reflections add two $a$ 's as neighbors, now
$$
4^{-1}(2 a+b+c) \equiv\left(2^{-1} a+2^{-1} a\right) \equiv a \quad(\bmod 5)
$$
In the three cases, any cell is still preserved modulo 5 after an operation. Hence we can fill in the $k r \times l s$ board by $k \times l$ copies by reflection.
Since 2|2018 and 3|2019, we can get through reflections the following board:
By the lemmas above, the board is invariant modulo 5, so the answer is no.
|
{
"problem_match": "\nProblem 4.",
"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl",
"solution_match": "\nSolution."
}
| 109
| 696
|
2019
|
T1
|
5
| null |
APMO
|
Determine all the functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f\left(x^{2}+f(y)\right)=f(f(x))+f\left(y^{2}\right)+2 f(x y)
$$
for all real number $x$ and $y$.
Answer: The possible functions are $f(x)=0$ for all $x$ and $f(x)=x^{2}$ for all $x$.
|
By substituting $x=y=0$ in the given equation of the problem, we obtain that $f(0)=0$. Also, by substituting $y=0$, we get $f\left(x^{2}\right)=f(f(x))$ for any $x$.
Furthermore, by letting $y=1$ and simplifying, we get
$$
2 f(x)=f\left(x^{2}+f(1)\right)-f\left(x^{2}\right)-f(1)
$$
from which it follows that $f(-x)=f(x)$ must hold for every $x$.
Suppose now that $f(a)=f(b)$ holds for some pair of numbers $a, b$. Then, by letting $y=a$ and $y=b$ in the given equation, comparing the two resulting identities and using the fact that $f\left(a^{2}\right)=f(f(a))=f(f(b))=f\left(b^{2}\right)$ also holds under the assumption, we get the fact that
$$
f(a)=f(b) \Rightarrow f(a x)=f(b x) \quad \text { for any real number } x
$$
Consequently, if for some $a \neq 0, f(a)=0$, then we see that, for any $x, f(x)=f\left(a \cdot \frac{x}{a}\right)=$ $f\left(0 \cdot \frac{x}{a}\right)=f(0)=0$, which gives a trivial solution to the problem.
In the sequel, we shall try to find a non-trivial solution for the problem. So, let us assume from now on that if $a \neq 0$ then $f(a) \neq 0$ must hold. We first note that since $f(f(x))=f\left(x^{2}\right)$ for all $x$, the right-hand side of the given equation equals $f\left(x^{2}\right)+f\left(y^{2}\right)+2 f(x y)$, which is invariant if we interchange $x$ and $y$. Therefore, we have
$$
f\left(x^{2}\right)+f\left(y^{2}\right)+2 f(x y)=f\left(x^{2}+f(y)\right)=f\left(y^{2}+f(x)\right) \quad \text { for every pair } x, y
$$
Next, let us show that for any $x, f(x) \geq 0$ must hold. Suppose, on the contrary, $f(s)=-t^{2}$ holds for some pair $s, t$ of non-zero real numbers. By setting $x=s, y=t$ in the right hand side of (2), we get $f\left(s^{2}+f(t)\right)=f\left(t^{2}+f(s)\right)=f(0)=0$, so $f(t)=-s^{2}$. We also have $f\left(t^{2}\right)=f\left(-t^{2}\right)=f(f(s))=f\left(s^{2}\right)$. By applying (2) with $x=\sqrt{s^{2}+t^{2}}$ and $y=s$, we obtain
$$
f\left(s^{2}+t^{2}\right)+2 f\left(s \cdot \sqrt{s^{2}+t^{2}}\right)=0
$$
and similarly, by applying (2) with $x=\sqrt{s^{2}+t^{2}}$ and $y=t$, we obtain
$$
f\left(s^{2}+t^{2}\right)+2 f\left(t \cdot \sqrt{s^{2}+t^{2}}\right)=0
$$
Consequently, we obtain
$$
f\left(s \cdot \sqrt{s^{2}+t^{2}}\right)=f\left(t \cdot \sqrt{s^{2}+t^{2}}\right)
$$
By applying (1) with $a=s \sqrt{s^{2}+t^{2}}, b=t \sqrt{s^{2}+t^{2}}$ and $x=1 / \sqrt{s^{2}+t^{2}}$, we obtain $f(s)=$ $f(t)=-s^{2}$, from which it follows that
$$
0=f\left(s^{2}+f(s)\right)=f\left(s^{2}\right)+f\left(s^{2}\right)+2 f\left(s^{2}\right)=4 f\left(s^{2}\right)
$$
a contradiction to the fact $s^{2}>0$. Thus we conclude that for all $x \neq 0, f(x)>0$ must be satisfied.
Now, we show the following fact
$$
k>0, f(k)=1 \Leftrightarrow k=1
$$
Let $k>0$ for which $f(k)=1$. We have $f\left(k^{2}\right)=f(f(k))=f(1)$, so by $(1), f(1 / k)=f(k)=$ 1 , so we may assume $k \geq 1$. By applying (2) with $x=\sqrt{k^{2}-1}$ and $y=k$, and using $f(x) \geq 0$, we get
$$
f\left(k^{2}-1+f(k)\right)=f\left(k^{2}-1\right)+f\left(k^{2}\right)+2 f\left(k \sqrt{k^{2}-1}\right) \geq f\left(k^{2}-1\right)+f\left(k^{2}\right) .
$$
This simplifies to $0 \geq f\left(k^{2}-1\right) \geq 0$, so $k^{2}-1=0$ and thus $k=1$.
Next we focus on showing $f(1)=1$. If $f(1)=m \leq 1$, then we may proceed as above by setting $x=\sqrt{1-m}$ and $y=1$ to get $m=1$. If $f(1)=m \geq 1$, now we note that $f(m)=f(f(1))=f\left(1^{2}\right)=f(1)=m \leq m^{2}$. We may then proceed as above with $x=\sqrt{m^{2}-m}$ and $y=1$ to show $m^{2}=m$ and thus $m=1$.
We are now ready to finish. Let $x>0$ and $m=f(x)$. Since $f(f(x))=f\left(x^{2}\right)$, then $f\left(x^{2}\right)=$ $f(m)$. But by (1), $f\left(m / x^{2}\right)=1$. Therefore $m=x^{2}$. For $x<0$, we have $f(x)=f(-x)=f\left(x^{2}\right)$ as well. Therefore, for all $x, f(x)=x^{2}$.
|
{
"problem_match": "\nProblem 5.",
"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl",
"solution_match": "\nSolution."
}
| 103
| 1,558
|
2020
|
T1
|
2
| null |
APMO
|
Show that $r=2$ is the largest real number $r$ which satisfies the following condition:
If a sequence $a_{1}, a_{2}, \ldots$ of positive integers fulfills the inequalities
$$
a_{n} \leq a_{n+2} \leq \sqrt{a_{n}^{2}+r a_{n+1}}
$$
for every positive integer $n$, then there exists a positive integer $M$ such that $a_{n+2}=a_{n}$ for every $n \geq M$.
|
. First, let us assume that $r>2$, and take a positive integer $a \geq 1 /(r-2)$.
Then, if we let $a_{n}=a+\lfloor n / 2\rfloor$ for $n=1,2, \ldots$, the sequence $a_{n}$ satisfies the inequalities
$$
\sqrt{a_{n}^{2}+r a_{n+1}} \geq \sqrt{a_{n}^{2}+r a_{n}} \geq \sqrt{a_{n}^{2}+\left(2+\frac{1}{a}\right) a_{n}} \geq a_{n}+1=a_{n+2}
$$
but since $a_{n+2}>a_{n}$ for any $n$, we see that $r$ does not satisfy the condition given in the problem.
Now we show that $r=2$ does satisfy the condition of the problem. Suppose $a_{1}, a_{2}, \ldots$ is a sequence of positive integers satisfying the inequalities given in the problem, and there exists a positive integer $m$ for which $a_{m+2}>a_{m}$ is satisfied.
By induction we prove the following assertion:
$$
a_{m+2 k} \leq a_{m+2 k-1}=a_{m+1} \text { holds for every positive integer } k
$$
The truth of $(\dagger)$ for $k=1$ follows from the inequalities below
$$
2 a_{m+2}-1=a_{m+2}^{2}-\left(a_{m+2}-1\right)^{2} \leq a_{m}^{2}+2 a_{m+1}-\left(a_{m+2}-1\right)^{2} \leq 2 a_{m+1}
$$
Let us assume that $(\dagger)$ holds for some positive integer $k$. From
$$
a_{m+1}^{2} \leq a_{m+2 k+1}^{2} \leq a_{m+2 k-1}^{2}+2 a_{m+2 k} \leq a_{m+1}^{2}+2 a_{m+1}<\left(a_{m+1}+1\right)^{2}
$$
it follows that $a_{m+2 k+1}=a_{m+1}$ must hold. Furthermore, since $a_{m+2 k} \leq a_{m+1}$, we have
$$
a_{m+2 k+2}^{2} \leq a_{m+2 k}^{2}+2 a_{m+2 k+1} \leq a_{m+1}^{2}+2 a_{m+1}<\left(a_{m+1}+1\right)^{2}
$$
from which it follows that $a_{m+2 k+2} \leq a_{m+1}$, which proves the assertion $(\dagger)$.
We can conclude that for the value of $m$ with which we started our argument above, $a_{m+2 k+1}=a_{m+1}$ holds for every positive integer $k$. Therefore, in order to finish the proof, it is enough to show that $a_{m+2 k}$ becomes constant after some value of $k$. Since every $a_{m+2 k}$ is a positive integer less than or equal to $a_{m+1}$, there exists $k=K$ for which $a_{m+2 K}$ takes the maximum value. By the monotonicity of $a_{m+2 k}$, it then follows that $a_{m+2 k}=a_{m+2 K}$ for all $k \geq K$.
|
{
"problem_match": "\nProblem 2.",
"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl",
"solution_match": "\nSolution 1"
}
| 121
| 844
|
2020
|
T1
|
3
| null |
APMO
|
Determine all positive integers $k$ for which there exist a positive integer $m$ and a set $S$ of positive integers such that any integer $n>m$ can be written as a sum of distinct elements of $S$ in exactly $k$ ways.
|
We claim that $k=2^{a}$ for all $a \geq 0$.
Let $A=\{1,2,4,8, \ldots\}$ and $B=\mathbb{N} \backslash A$. For any set $T$, let $s(T)$ denote the sum of the elements of $T$. (If $T$ is empty, we let $s(T)=0$.)
We first show that any positive integer $k=2^{a}$ satisfies the desired property. Let $B^{\prime}$ be a subset of $B$ with $a$ elements, and let $S=A \cup B^{\prime}$. Recall that any nonnegative integer has a unique binary representation. Hence, for any integer $t>s\left(B^{\prime}\right)$ and any subset $B^{\prime \prime} \subseteq B^{\prime}$, the number $t-s\left(B^{\prime \prime}\right)$ can be written as a sum of distinct elements of $A$ in a unique way. This means that $t$ can be written as a sum of distinct elements of $B^{\prime}$ in exactly $2^{a}$ ways.
Next, assume that some positive integer $k$ satisfies the desired property for a positive integer $m \geq 2$ and a set $S$. Clearly, $S$ is infinite.
Lemma: For all sufficiently large $x \in S$, the smallest element of $S$ larger than $x$ is $2 x$.
Proof of Lemma: Let $x \in S$ with $x>3 m$, and let $x<y<2 x$. We will show that $y \notin S$. Suppose first that $y>x+m$. Then $y-x$ can be written as a sum of distinct elements of $S$ not including $x$ in $k$ ways. If $y \in S$, then $y$ can be written as a sum of distinct elements of $S$ in at least $k+1$ ways, a contradiction. Suppose now that $y \leq x+m$. We consider $z \in(2 x-m, 2 x)$. Similarly as before, $z-x$ can be written as a sum of distinct elements of $S$ not including $x$ or $y$ in $k$ ways. If $y \in S$, then since $m<z-y<x, z-y$ can be written as a sum of distinct elements of $S$ not including $x$ or $y$. This means that $z$ can be written as a sum of distinct elements of $S$ in at least $k+1$ ways, a contradiction.
We now show that $2 x \in S$; assume for contradiction that this is not the case. Observe that $2 x$ can be written as a sum of distinct elements of $S$ including $x$ in exactly $k-1$ ways. This means that $2 x$ can also be written as a sum of distinct elements of $S$ not including $x$. If this sum includes any number less than $x-m$, then removing this number, we can write some number $y \in(x+m, 2 x)$ as a sum of distinct elements of $S$ not including $x$. Now if $y=y^{\prime}+x$ where $y^{\prime} \in(m, x)$ then $y^{\prime}$ can be written as
a sum of distinct elements of $S$ including $x$ in exactly $k$ ways. Therefore $y$ can be written as a sum of distinct elements of $S$ in at least $k+1$ ways, a contradiction. Hence the sum only includes numbers in the range $[x-m, x)$. Clearly two numbers do not suffice. On the other hand, three such numbers sum to at least $3(x-m)>2 x$, a contradiction.
From the Lemma, we have that $S=T \cup U$, where $T$ is finite and $U=\{x, 2 x, 4 x, 8 x, \ldots\}$ for some positive integer $x$. Let $y$ be any positive integer greater than $s(T)$. For any subset $T^{\prime} \subseteq T$, if $y-s\left(T^{\prime}\right) \equiv 0(\bmod x)$, then $y-s\left(T^{\prime}\right)$ can be written as a sum of distinct elements of $U$ in a unique way; otherwise $y-s\left(T^{\prime}\right)$ cannot be written as a sum of distinct elements of $U$. Hence the number of ways to write $y$ as a sum of distinct elements of $S$ is equal to the number of subsets $T^{\prime} \subseteq T$ such that $s\left(T^{\prime}\right) \equiv y(\bmod x)$. Since this holds for all $y$, for any $0 \leq a \leq x-1$ there are exactly $k$ subsets $T^{\prime} \subseteq T$ such that $s\left(T^{\prime}\right) \equiv a(\bmod x)$. This means that there are $k x$ subsets of $T$ in total. But the number of subsets of $T$ is a power of 2 , and therefore $k$ is a power of 2 , as claimed.
|
{
"problem_match": "\nProblem 3.",
"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl",
"solution_match": "# Solution:"
}
| 55
| 1,164
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.